

分析 (1)先过点A作AC⊥x轴于C,作BD⊥x轴于D,得出AC=6,BD=2=CO=DO,进而得到CD=4,最后根据△ABO的面积=梯形ABDC的面积-△ACO的面积-△BDO的面积,进行计算即可;
(2)设P(x,0),分两种情况进行讨论:当点P在直线AB的左侧时,△APB的面积=梯形ACDB的面积-△ACP的面积-△BDP的面积;当点P在直线AB的右侧时,△APB的面积=△ACP的面积-△ACO的面积-△AOB的面积-△BOP的面积,分别列出关于x 方程,求得x的值即可得到P点坐标;
(3)连接DE,根据三角形内角和定理以及角平分线的定义,求得∠FED+∠FDE=30°,进而根据△DEF中,∠DFE=180°-(∠FED+∠FDE)进行计算,即可得出∠DFE的值.
解答 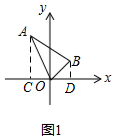 解:(1)如图1,过点A作AC⊥x轴于C,作BD⊥x轴于D,则AC=6,BD=2=CO=DO,
解:(1)如图1,过点A作AC⊥x轴于C,作BD⊥x轴于D,则AC=6,BD=2=CO=DO,
∴CD=4,
∴△ABO的面积=梯形ABDC的面积-△ACO的面积-△BDO的面积
=$\frac{1}{2}$(2+6)×4-$\frac{1}{2}$×2×6-$\frac{1}{2}$×2×2
=16-6-2
=8;
(2)存在点P,使△ABP的面积等于6.
设P(x,0),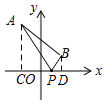
如图所示,当点P在直线AB的左侧时,△APB的面积=梯形ACDB的面积-△ACP的面积-△BDP的面积,
∵△ABP的面积等于6,
∴6=$\frac{1}{2}$(2+6)×4-$\frac{1}{2}$×6×(x+2)-$\frac{1}{2}$×2×(2-x),
解得x=1,
∴P(1,0);
如图所示,当点P在直线AB的右侧时,△APB的面积=△ACP的面积-△ACO的面积-△AOB的面积-△BOP的面积,
∵△ABP的面积等于6,△ABO的面积=8,
∴6=$\frac{1}{2}$×6×(x+2)-$\frac{1}{2}$×2×6-8-$\frac{1}{2}$×2×x,
解得x=7,
∴P(7,0),
综上所述,点P的坐标为(1,0)或(7,0);
(3)如图3,连接DE,
∵∠A=30°,
∴∠AED+∠ADE=180°-30°=150°,
∵∠DOE=90°,
∴∠OED+∠ODE=90°,
∴∠AEO+∠ADO=150°-90°=60°,
∵x轴、y轴分别平分∠ADF、∠AEF,
∴∠OEF=∠AEO,∠ODF=∠ADO,
∴∠OEF+∠ODF=∠AEO+∠ADO=60°,
又∵∠OED+∠ODE=90°,
∴∠FED+∠FDE=90°-60°=30°,
∴△DEF中,∠DFE=180°-(∠FED+∠FDE)=180°-30°=150°.
点评 本题属于三角形综合题,主要考查了三角形内角和定理,角平分线的定义,以及三角形的面积计算公式的综合应用,解决问题的关键是中辅助线构造构造三角形,根据图形之间的面积关系进行求解.解题时注意:第(3)问也可以通过作辅助线,根据三角形外角性质进行计算求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为1,E是边AB上一点,且AE=$\frac{1}{3}$,点F在边BC上,且BF=$\frac{1}{3}$,一束光线从点E射入到点F,若光线每碰到正方形的边时都会发生镜面反射.反射时反射角等于入射角,当光线再次经过点E时,光线发生反射的次数可能为( )
如图,正方形ABCD的边长为1,E是边AB上一点,且AE=$\frac{1}{3}$,点F在边BC上,且BF=$\frac{1}{3}$,一束光线从点E射入到点F,若光线每碰到正方形的边时都会发生镜面反射.反射时反射角等于入射角,当光线再次经过点E时,光线发生反射的次数可能为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,且c=d,则ac>bd | B. | 若ac>bc,则a>b | ||
| C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,图2均为3×3方格,在图1中,已知各行、各列及对角线上三个数之和都等于15,试求x、y的值,并把满足已知条件的另外8个数字填入图2的方格内.
如图1,图2均为3×3方格,在图1中,已知各行、各列及对角线上三个数之和都等于15,试求x、y的值,并把满足已知条件的另外8个数字填入图2的方格内.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com