
��ͼ,������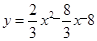 ��x�ύ��A��C����,��y�ύ��B�㣮
��x�ύ��A��C����,��y�ύ��B�㣮

��1�����AOB�����Բ�������
��2��������P�ӵ�A����,��ÿ��1����λ������AC�����˶���ͬʱ,��Q�ӵ�B����,��ÿ��0.5����λ������BA�����˶�,����P�����C��ʱ,����ͬʱֹͣ�˶����ʵ�tΪ��ֵʱ,��A��P��QΪ��������������OAB���ƣ�
��3����MΪ�߶�AB��һ������,����M��MNƽ����y�ύ�������ڵ�N��
�ʣ��Ƿ���������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı��Σ�������,�����M�����ꣻ��������,��˵�����ɣ�
��1��25�У���2��t�� ��A��P��QΪ��������������OAB���ƣ���3�������������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı���,���ɼ�������
��A��P��QΪ��������������OAB���ƣ���3�������������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı���,���ɼ�������
��������
���������(1)�����A,B����,���AOB�����Բ�İ뾶Ϊ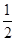 AB,����Բ�������ʽ��⼴�ɣ�
AB,����Բ�������ʽ��⼴�ɣ�
��2���������������ζ�Ӧ�ߵı�����г�����ʽ,��⼴�ɣ�
��3�����ı���OMNBΪƽ���ı���,����ƽ���ı��ε����ʵó�MN=OB=8,�ݴ��г�����( x��8)��(
x��8)��( x2��
x2��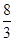 x��8)��8,���б�ʽ����0�����жϳ������������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı��Σ�
x��8)��8,���б�ʽ����0�����жϳ������������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı��Σ�
�����������1���� ,
,
�൱y=0ʱ,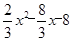 =0,���x=6��8,
=0,���x=6��8,
��A��6,0��,B��0,��8��
��OA��6,OB��8,��AB��10
��S����(5)2��25��
��2��AP��t,AQ��10��0.5t,����AC=8,��0��t��8
����APQ�ס�AOB,�� ����t��
����t�� ��
��
����AQP�ס�AOB,��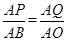 ����t��
����t�� ��8����ȥ,����
��8����ȥ,����
�൱t�� ʱ,��A��P��QΪ��������������OAB���ƣ�
ʱ,��A��P��QΪ��������������OAB���ƣ�
��3��ֱ��AB�ĺ�����ϵʽΪ ��
��
��MN��y��
�����M�ĺ�����Ϊx,��M��x, x��8��,N��x,
x��8��,N��x, x2��
x2��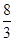 x��8����
x��8����
���ı���OMNBΪƽ���ı���,��MN��OB��8
��( x��8)��(
x��8)��( x2��
x2��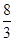 x��8)��8
x��8)��8
��x2��6x��12��0
�ߡ���0,��˷�����ʵ����,
����������ĵ�M,ʹ���ı���OMNBǡΪƽ���ı��Σ�
���㣺���κ����ۺ��⣮


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
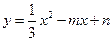 ��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��
��x�ύ��A��B���㣬��y�ύ�ڵ�C��0�� �����ҶԳƳ�x=l��
�����ҶԳƳ�x=l��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ۺ���̽������ͼ,������![]() ��x�ύ��A,B����(��B�ڵ�A���Ҳ�)��y�ύ�ڵ�C,����BC,��BCΪһ��,��OΪ�Գ�����������BDEC,��P��x���ϵ�һ������,���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q
��x�ύ��A,B����(��B�ڵ�A���Ҳ�)��y�ύ�ڵ�C,����BC,��BCΪһ��,��OΪ�Գ�����������BDEC,��P��x���ϵ�һ������,���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q

��1�����A,B,C�����ꡣ
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M,N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɡ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ� Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ ���ͣ������
��ͼ������ ��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��
��x�ύ��A��B���㣬��y�ύ�ڵ�C��0�� �����ҶԳƳ�x=l��
�����ҶԳƳ�x=l��
��1����������ߵĽ���ʽ��A��B��������ꣻ
��2����x���·������������Ƿ���ڵ�D��ʹ�ı���ABDC�����Ϊ3�������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�ʹ��ͼ1����
��3����Q��y���ϣ���P���������ϣ�ҪʹQ��P��A��BΪ������ı�����ƽ���ı��Σ�������������������ĵ�P�����꣨ʹ��ͼ2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ʡ���꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��ͼ,������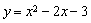 ��x�ύ��A��B����,��y�ύ�ڵ�C��
��x�ύ��A��B����,��y�ύ�ڵ�C��
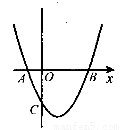
��1���ֱ������A��B��C������;
��2����������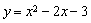 �Ķ���ΪM,���ı���ABMC�������
�Ķ���ΪM,���ı���ABMC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ�ɽ��������ѧ�������棩 ���ͣ������
�ۺ���̽������ͼ,������ ��x�ύ��A,B����(��B�ڵ�A���Ҳ�)��y�ύ�ڵ�C,����BC,��BCΪһ��,��OΪ�Գ�����������BDEC,��P��x���ϵ�һ������,���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��x�ύ��A,B����(��B�ڵ�A���Ҳ�)��y�ύ�ڵ�C,����BC,��BCΪһ��,��OΪ�Գ�����������BDEC,��P��x���ϵ�һ������,���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��

��1�����A,B,C�����ꡣ
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M,N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɡ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ� Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com