a、b为实数,关于x的方程x2+ax+b=2和x2+ax+b=-2共有三个不相等的实数根:
(1)求证:a2-4b-8=0
(2)若该方程的三个不相等的实数根恰为一直角三角形的三边长,求此三角形的三边的长度.
【答案】
分析:(1)由于关于x的方程x
2+ax+b=2和x
2+ax+b=-2共有三个不相等的实数根,所以有三种情况:
①两个方程都有不相等的两个实数根,但两个方程有一个相同的根;
②第一个方程有两个不同的实数根,第二个方程有两个相等的实数根;
③第一个方程有两个相同的实数根,第二个方程有两个不相等的实数根;然后结合方程的形式讨论其中只有②成立,由此即可证明题目的结论;
(2)利用(1)知道第一个方程有两个不同的实数根,第二个方程有两个相等的实数根,然后利用根与系数的关系及已知条件即可求出结果.
解答:解:(1)∵关于x的方程x
2+ax+b=2和x
2+ax+b=-2共有三个不相等的实数根,
∴有三种情况:
①两个方程都有不相等的两个实数根,但两个方程有一个相同的根;
设相同的根是t,将t代入这组方程得到,
t
2+at+b=2
t
2+at+b=-2
这种情况不可能,所以排除;
②第一个方程有两个不同的实数根,第二个方程有两个相等的实数根;
此时x
2+ax+b=-2可以变为x
2+ax+b+2=0,
∴△=a
2-4b-8=0;
③第一个方程有两个相同的实数根,第二个方程有两个不相等的实数根,
此时x
2+ax+b=2可以变为x
2+ax+b-2=0,
∴△=a
2-4b+8=0,
设x
1=x
2=t,
∴x
1+x
2=-a,x
1x
2=b-2,
第二个方程中设x
3和x
4是方程的根,
∴x
3+x
4=-a,x
3x
4=b+2,
∵x
1x
2=b-2,
∴t=
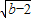
,
∴x
3+x
4=-a=2
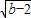
,x
3x
4=b+2,
由这组关系式用韦达定理可以将x
3,x
4看做方程
x
2-2
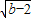
x+b+2=0的解,
然而x
2-2
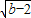
x+b+2=(x-2
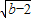
)
2+4,这个关系式大于0,
所以该方程无解,也就是第三种情况不存在;
(2)∵第二种情况存在,
设x
1、x
2是第一个方程的根,x
3、x
4是第二个方程的根
∴由韦达定理知x
1+x
2=-a,x
1x
2=b-2,x
3+x
4=-a,x
3x
4=b+2.
设x
3=x
4=t(t>0)
那么t
2=b+2,得t=
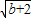
,
∵a
2-4b-8=0,
∴a
2=4b+8,
∴a=-2
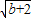
,
∴x
1+x
2=2
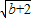
,x
1x
2=b-2,
解得x
1=
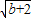
+2,x
2=
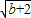
-2
∵x
1,x
2,t构成直角三角形三条边,
∴(
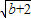
+2)
2=(
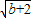
-2)
2+(
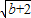
)
2
解得b=62,
∴x
1=
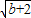
+2=8+2=10,
x
2=
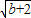
-2=8-2=6,
t=
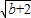
=8;
故直角三角形三条边长分别是6,8,10(从小到大).
点评:此题比较难,综合考查了一元二次方程的根的定义,判别式,根与系数的关系等知识,同时也考查了分类讨论的数学思想,对于学生分析问题解决问题的能力要求比较高,所以平时要加强训练.

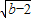 ,
,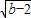 ,x3x4=b+2,
,x3x4=b+2,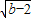 x+b+2=0的解,
x+b+2=0的解,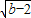 x+b+2=(x-2
x+b+2=(x-2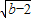 )2+4,这个关系式大于0,
)2+4,这个关系式大于0,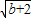 ,
,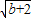 ,
,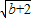 ,x1x2=b-2,
,x1x2=b-2,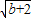 +2,x2=
+2,x2=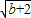 -2
-2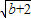 +2)2=(
+2)2=(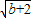 -2)2+(
-2)2+(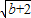 )2
)2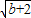 +2=8+2=10,
+2=8+2=10,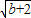 -2=8-2=6,
-2=8-2=6,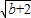 =8;
=8;
