
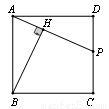
如图,边长为5的正方形ABCD,点P为边CD上一点,连接AP,过点B作BH⊥AP,若 ∠ABH的正切值为 ,则线段HP= .
,则线段HP= .
 .
.
【解析】
试题分析:根据同角的余角相等求出∠DAP=∠ABH,然后求出DP,再利用勾股定理列式求出AP,设AH=x,表示出BH=2x,利用勾股定理列式求出x,然后根据HP=AP-AH代入数据进行计算即可得解.
试题解析:在正方形ABCD中,∠BAD=90°,
∴∠BAH+DAP=90°,
∵BH⊥AP,
∴∠ABH+∠BAH=90°,
∴∠DAP=∠ABH,
∴DP=AD•tan∠DAP=5×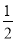 =
= ,
,
由勾股定理得,AP=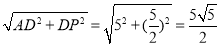
设AH=x,
∵∠ABH的正切值为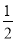 ,
,
∴BH=2x,
在Rt△ABH中,AH2+BH2=AB2,
即x2+(2x)2=52,
解得x= ,
,
∴HP=AP-AH= .
.
考点:1.正方形的性质;2.勾股定理;3.解直角三角形.


科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,C.D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠BOC=( )
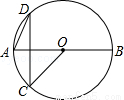
A.25° B.50° C.130° D.155°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省耒阳市九年级上学期期末考试数学试卷(解析版) 题型:选择题
下列多边形一定相似的为( )
A.两个三角形 B.两个四边形 C.两个正方形 D.两个平行四边形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:解答题
如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E.
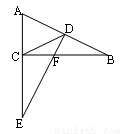
(1)求证:∠A=∠F;
(2)△CDE与△FDC是否相似?并给予证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:选择题
已知抛物线的解析式为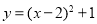 ,则当 x≥2时,y随x增大的变化规律是( )
,则当 x≥2时,y随x增大的变化规律是( )
A.增大 B.减小 C.先增大再减小 D.先减小后增大
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:填空题
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为 .
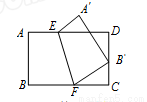
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
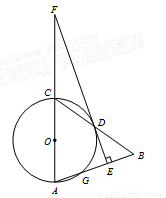
(1)求证:直线EF是⊙O的切线;
(2)CF=5,cos∠A =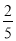 ,求BE的长.[来~源#:*中&教网%]
,求BE的长.[来~源#:*中&教网%]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com