
分析 先利用绝对值的意义得到a=±3,b=±5,
①当a与b异号时,则a=3,b=-5或a=-3,b=5,然后分别计算a-b的值;
③由于|a+b|=-(a+b),则a+b<0,所以a=3,b=-5或a=-3,b=-5,然后分别计算a-b的值.
解答 解:∵|a|=3,|b|=5,
∴a=±3,b=±5,
①∵a•b<0,
∴a=3,b=-5或a=-3,b=5,
当a=3,b=-5,a-b=3-(-5)=8,
当a=-3,b=5,a-b=-3-5=-8;
③∵|a+b|=-(a+b),
∴a=3,b=-5或a=-3,b=-5,
当a=3,b=-5,a-b=3-(-5)=8,
当a=-3,b=-5,a-b=-3+5=2.
点评 本题考查了有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘. 也考查了绝对值的意义.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
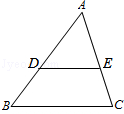 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
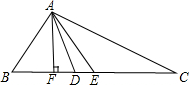 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com