
【题目】利用函数图象探究方程x(|x|﹣2)=![]() 的实数根的个数.
的实数根的个数.
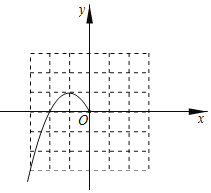
(1)设函数y=x(|x|﹣2),则这个函数的图象与直线y=![]() 的交点的横坐标就是方程x(|x|﹣2)=
的交点的横坐标就是方程x(|x|﹣2)=![]() 的实数根.
的实数根.
(2)分类讨论:当x≤0时,y=﹣x2﹣2x;当x>0时,y= ;
(3)在给定的坐标系中,已经画出了当x≤0时的函数图象,请根据(2)中的解析式,通过描点,连线,画出当x>0时的函数图象.
(4)在给定的坐标系中画直线y=![]() 、观察图象可知方程x(|x|﹣2)=
、观察图象可知方程x(|x|﹣2)=![]() 的实数根有 个.
的实数根有 个.
(5)深入探究:若关于x的方程2x(|x|﹣2)=m有三个不相等的实数根,且这三个实数根的和为负数,则m的取值范围是 .
【答案】(1)函数y=x(|x|﹣2)的图象与直线y=![]() 的交点的横坐标就是方程x(|x|﹣2)=
的交点的横坐标就是方程x(|x|﹣2)=![]() 的实数根;(2)x2﹣2x;(3)如图,见解析;(4)3;(5)﹣2≤m<0.
的实数根;(2)x2﹣2x;(3)如图,见解析;(4)3;(5)﹣2≤m<0.
【解析】
(1)函数y=x(|x|﹣2)的图象与直线y=![]() 的交点的横坐标就是方程x(|x|﹣2)=
的交点的横坐标就是方程x(|x|﹣2)=![]() 的实数根.
的实数根.
(2)根据绝对值的性质去掉绝对值整理即可,注意x的取值范围;
(3)通过描点,连线,画出当x>0时的函数图象即可;
(4)根据两个函数图象交点的个数,找出方程解的个数;
(5)根据两个函数图象相交产生的交点,比较交点横坐标的特征,加以分析即可求得.
解:(1)函数y=x(|x|﹣2)的图象与直线y=![]() 的交点的横坐标就是方程x(|x|﹣2)=
的交点的横坐标就是方程x(|x|﹣2)=![]() 的实数根.
的实数根.
(2)当x>0时,y=x(|x|﹣2)=x(x﹣2)=x2﹣2x,
故答案为x2﹣2x;
(3)如图:
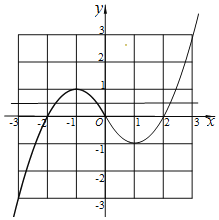
(4)如(3)题图,直线y=![]() 的图象与y=x(|x|﹣2)的图象有三个交点,则可知方程x(|x|﹣2)=
的图象与y=x(|x|﹣2)的图象有三个交点,则可知方程x(|x|﹣2)=![]() 的实数根有 3个.
的实数根有 3个.
故答案为3;
(5)根据题意画出图象:

直线y=m与函数y=x(|x|﹣2)的交点的横坐标x1<0<x2<x3,且x2+x3=2,x1≤﹣2,
∴x1+x2+x3≤0,
∴﹣2≤m<0
∴关于x的方程x(|x|﹣2)=即2x(|x|﹣2)=m有三个不相等的实数根,且这三个实数根的和为非负数,则m的取值范围是﹣2≤m<0,
故答案为﹣2≤m<0.


科目:初中数学 来源: 题型:
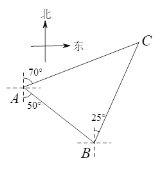
【题目】如图,轮船在A处观测灯塔C位于北偏东70o方向上,轮船从A处以每小时30海里的速度沿南偏东50o方向匀速航行,1小时后到达码头B处,此时观测灯塔C位于北偏东25o方向上,求灯塔C与码头B之间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
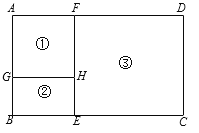
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
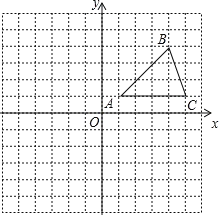
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
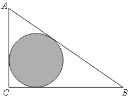
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与x轴交于点C,与反比例函数
与x轴交于点C,与反比例函数![]() 交于点
交于点![]() 和点B.
和点B.

(1)求反比例函数表达式及点B的坐标;
(2)点P是x轴上的一点,若![]() 的面积是6,求点P的坐标.
的面积是6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com