
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
【答案】D
【解析】
分为两种情况:①当△ABE在正方形ABCD外时,过E作EM⊥AB于M,根据
等边三角形性质求出AM、AE,根据勾股定理求出EM,即可得出E的坐标,求出∠EAD,
根据三角形的内角和定理和等腰三角形性质即可求出∠ADE;②当等边△ABE在正方形
ABCD内时,同法求出此时E的坐标,求出∠DAE,根据三角形的内角和定理和等腰三角
形性质即可求出∠ADE.
分为两种情况:①△ABE在正方形ABCD外时,如图,过E作EM⊥AB于M,
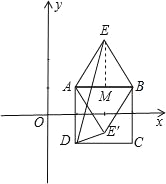
∵等边三角形ABE,
∴AE=AB=3﹣1=2,
∴AM=1,
由勾股定理得:AE2=AM2+EM2,
∴22=12+EM2,
∴![]()
∵A(1,1),
∴E的坐标是![]()
∵等边△ABE和正方形ABCD,
∴∠DAB=90°,∠EAB=60°,AD=AE,
∴![]()
②同理当△ABE在正方形ABCD内时,同法求出E的坐标是![]()
∵∠DAE=90°﹣60°=30°,
AD=AE,
∴![]()
∴∠ADE和点E的坐标分别为15°,![]() 或75°,
或75°,![]()
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 ![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )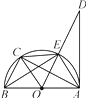
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为30cm,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=11cm,则DE的长为____cm.
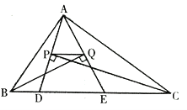
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期日早晨,小青从家出发匀速去森林公园溜冰,小青出发一段时间后,他妈妈发现小青忘带了溜冰鞋,于是立即骑自行车沿小青行进的路线匀速去追赶,妈妈追上小青后,立即沿原路线匀速返回家,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的三分之二,小青继续以原速度步行前往森林公园,妈妈与小青之间的路程![]() 米
米![]() 与小青从家出发后步行的时间
与小青从家出发后步行的时间![]() 分
分![]() 之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米
之间的关系如图所示,当妈妈刚回到家时,小青到森林公园的路程还有______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:![]() 为常数,且
为常数,且![]() 经过第四象限.
经过第四象限.

(1)若直线l与x轴交于点![]() ,求m的值;
,求m的值;
(2)求m的取值范围:
(3)判断点![]() 是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由.
是否在直线l上,若不在,判断在直线l的上方还是下方?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一只电子狗从原点O出发,按向上→向右→向下→向下→向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,则A3020的坐标为( )

A.(1007,1)B.(1007,﹣1)C.(504,1)D.(504,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)请你利用上面的结论计算:
299+298+297+…+2+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 为⊙
为⊙ ![]() 的弦,过点
的弦,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() .点
.点 ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)求证:直线 ![]() 是⊙
是⊙ ![]() 的切线;
的切线;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
解:设![]() .
.
方程两边都乘以10,可得![]() .
.
由![]() 和
和![]() ,可得
,可得![]() 即
即![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
解得![]() ,即
,即![]() .
.
填空:将0.![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把小数1.![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com