
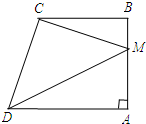
 如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.
如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.分析 (1)过点M作MN∥AD(如图),根据平行线的性质得到∠DMN=∠ADM,∠CMN=∠BCM,于是得到∠DMN+∠CMN=∠ADM+∠BCM,即可得到结论;
(2)根据勾股定理得到MD=$\sqrt{{6^2}+{8^2}}=10$,由于CD=CM=$5\sqrt{2}$,于是得到$C{D^2}+C{M^2}={(5\sqrt{2})^2}+{(5\sqrt{2})^2}=100=D{M^2}$,即可得到结论;
(3)连结AC,过点C作CE⊥AD于点E,根据平行线的性质得到∠B=∠BAD=90°,根据余角的性质得到∠DCE=∠MCB,推出△CDE≌△CMB,根据全等三角形的性质得到CE=CB,S△CDE=S△CMB,由S四边形ABCE=S△CBM+S四边形AMCE,S四边形AMCD=S△CDE+S四边形AMCE,得到S四边形ABCE=S四边形AMCD=49,通过Rt△ACE≌Rt△ACB,得到∠ACB=∠ACE=45°,S△ACE=S△ACB=$\frac{49}{2}$,于是得到结论.
解答 (1)证明:过点M作MN∥AD(如图),
∴∠DMN=∠ADM,
∵AD∥BC,
∴MN∥BC,
∴∠CMN=∠BCM,
∴∠DMN+∠CMN=∠ADM+∠BCM,
即∠CMD=∠BCM+∠ADM;
(2)解:∵AD=8,AM=6,∠BAD=90°,
∴MD=$\sqrt{{6^2}+{8^2}}=10$,
∵CD=CM=$5\sqrt{2}$,
∴$C{D^2}+C{M^2}={(5\sqrt{2})^2}+{(5\sqrt{2})^2}=100=D{M^2}$,
∴△CDM为直角三角形,且∠DCM=90°,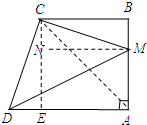
∴S四边形AMCD=S△CDM+S△ADM=$\frac{1}{2}×6×8+\frac{1}{2}×{(5\sqrt{2})^2}=49$;
(3)解:连结AC,过点C作CE⊥AD于点E,
∵AD∥BC,
∴∠B=∠BAD=90°,
∵CE⊥AD,
∴∠CED=∠BCE=90°,
∴∠B=∠CED,
∵∠DCM=90°,∠BCE=90°,
即∠DCE+∠ECM=90°∠BCM+∠ECM=90°,
∴∠DCE=∠MCB,
在△CDE与△CMB中,$\left\{\begin{array}{l}{∠CED=∠B=90°}\\{∠DCE=∠BCM}\\{CD=CM}\end{array}\right.$,
∴△CDE≌△CMB,
∴CE=CB,S△CDE=S△CMB,
∵S四边形ABCE=S△CBM+S四边形AMCE,S四边形AMCD=S△CDE+S四边形AMCE,
∴S四边形ABCE=S四边形AMCD=49,
在Rt△ACE与Rt△ACB中,$\left\{\begin{array}{l}{CE=CB}\\{AC=AC}\end{array}\right.$,
∴Rt△ACE≌Rt△ACB,
∴∠ACB=∠ACE=45°,S△ACE=S△ACB=$\frac{49}{2}$,
∵∠B=90°,∴∠ACB=∠CAB=45°,
∴AB=BC,
∵S△ACB=$\frac{49}{2}$,∴$\frac{1}{2}×A{B^2}=\frac{49}{2}$,
∴AB=7,
∴AC=$\sqrt{{7^2}+{7^2}}=7\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,勾股定理,三角形的面积的计算,正确的作出辅助线是解题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
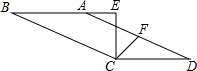 如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.
如图,已知?ABCD中,点F为AD的中点,CE⊥AB交BA的延长线于点E,连CF,若∠ECF=45°,试写出CD、AE、CE的数量关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com