
如图,反比例函数 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
(3)求△AOB的面积.
(1)y=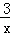 y=x+2
y=x+2
(2)x<﹣3或0<x<1
(3)4
解析试题分析:(1)把A(1,3)代入反比例函数 即可得到k=3,然后把B(n,﹣1)代入y=
即可得到k=3,然后把B(n,﹣1)代入y=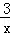 求出n,再把A点和B点坐标代入y=mx+b中得到关于m、b的方程组,然后解方程组即可;
求出n,再把A点和B点坐标代入y=mx+b中得到关于m、b的方程组,然后解方程组即可;
(2)观察图象可得到当x<﹣3或0<x<1时,反比例函数的图象都在一次函数的图象的上方;
(3)先求出直线AB与x轴的交点C的坐标,则S△OAB=S△OAC+S△OBC,然后利用三角形的面积公式计算即可.
解:(1)把A(1,3)代入反比例函数 ,
,
∴k=1×3=3,
∴反比例函数的解析式为y=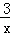 ,
,
把B(n,﹣1)代入y=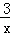 得,n=﹣3,
得,n=﹣3,
∴点B的坐标为(﹣3,﹣1),
把A(1,3)、点B(﹣3,﹣1)代入一次函数y=mx+b得,m+b=3,﹣3m+b=﹣1,解得m=1,b=2,
∴一次函数的解析式为y=x+2;
(2)当x<﹣3或0<x<1时,反比例函数的值大于一次函数的值;
(3)连OA、OB,直线AB交x轴与C点,如图,
对于y=x+2,令y=0,x=﹣2,
∴C点坐标为(﹣2,0),
∴S△OAB=S△OAC+S△OBC= ×2×3+
×2×3+ ×2×1=4.
×2×1=4.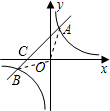
点评:本题考查了反比例函数与一次函数的交点问题:同时满足反比例函数的解析式和一次函数的解析式的点的坐标为它们图象的交点坐标.也考查了待定系数法求函数的解析式以及坐标轴上点的坐标特点.


科目:初中数学 来源: 题型:解答题
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、A(0,3),反比例函数的图象经过点C.
(1)求C点坐标和反比例函数的解析式;(6分)
(2)将等腰梯形ABCD向上平移 个单位后,使点B恰好落在双曲线上,求
个单位后,使点B恰好落在双曲线上,求 的值.(4分)
的值.(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).
(1)求m的值;
(2)求正比例函数y=kx的解析式;
(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线AB与y轴、x轴分别交于点A、点B,与双曲线 交于点C(1,6)、D(3,n)两点,
交于点C(1,6)、D(3,n)两点, 轴于点E,
轴于点E, 轴于点F.
轴于点F.
(1)填空: ,
, ;
;
(2)求直线AB的解析式;
(3)求证: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=-x的图像与反比例函数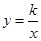 的图象交于A、B两点。
的图象交于A、B两点。
①根据图象求K的值
②点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,试写出点P所有可能的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀,摸球的人都蒙上眼睛.先甲无放回摸两次,每次摸出一个球;再把甲摸出的两个球同时放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)(4分)运用列表或画树状图求甲得1分的概率;
(2)(4分)这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=70°,则∠2的度数是( )
A.70° B.55° C.60° D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)(4分)左下图是有几个大小完全一样的小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,请你画出该几何体的主视图和左视图.

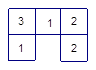
|
|
 的边OB上的一点
的边OB上的一点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com