
【题目】现有20箱苹果,以每箱25千克为标准,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如表:
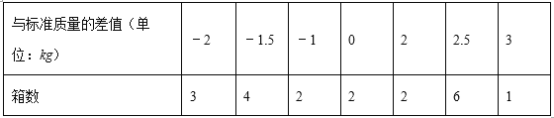
(1)20箱苹果中,最重的一箱比最轻的一箱重 kg;
(2)与标准质量相比,20箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价12元,则售出这20箱苹果可获得多少元?
【答案】(1)5;(2)8千克;(3)6096元
【解析】
(1)因为表格中表示的各箱重量的标准数相同,都为25千克,只考虑与标准的质量差值即可,找出最重的为+3,最轻的为-2,两者相减即可求出;
(2)根据表格中的数据,利用总重量与标准数的差乘以相应的箱数,并把乘得的结果相加,求出的和若为正表明超过标准重量,若和为负,表明不足标准重量;
(3)用每一箱的标准数25乘以箱数20,再加上(2)求出的数字即为总重量,然后乘以单价即可求出卖得钱数.
(1)3﹣(﹣2)=5(千克),
答:最重的一箱比最轻的一箱多重5千克,
故答案为:5;
(2)(﹣2×3)+(﹣1.5×4)+(﹣1×2)+(0×2)+(2×2)+(2.5×6)+(3×1)
=﹣6﹣6﹣2+0+4+15+3
=8(千克),
答:与标准质量比较,这20箱苹果总计超过8千克;
(3)20箱苹果的总质量为:25×20+8=508(千克),
508×12=6096(元),
答:出售这20箱苹果可卖6096元.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
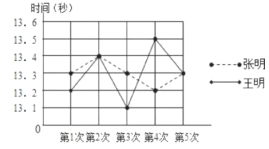
【题目】为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”短跑运动可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
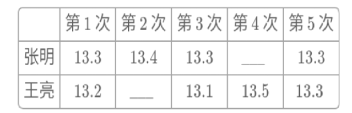
(1)请根据图中信息,补齐下面的表格;
(2)从图中看,小明与小亮哪次的成绩最好?
(3)分别计算他们的平均数和方差,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:三角形的一条中位线与第三边上的中线互相平分.
要求:(1)根据给出的![]() 和它的一条中位线
和它的一条中位线![]() ,在给出的图形上,请用尺规作出
,在给出的图形上,请用尺规作出![]() 边上的中线
边上的中线![]() ,交
,交![]() 于点
于点![]() .不写作法,保留痕迹;
.不写作法,保留痕迹;
(2)据此写出已知,求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
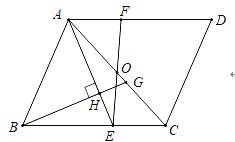
【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点F.过点
于点F.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
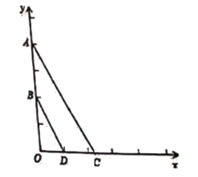
【题目】已知:如图,平面直角坐标系中,![]() ,
,![]() ,点C是x轴上一点,点D为OC的中点.
,点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于2,求点C的坐标;
(3)如果![]() 于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
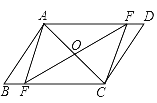
【题目】如图所示,AC是ABCD的一条对角线,过AC中点O的直线EF分别交AD,BC于点E,F.
(1)求证:△AOE≌△COF;
(2)连接AF和CE,当EF⊥AC时,判断四边形AFCE的形状,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com