
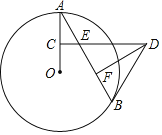
【题目】如图,AB是⊙O的一条弦,点C是半径OA的中点,过点C作OA的垂线交AB于点E,且与BE的垂直平分线交于点D,连接BD.
(1)求证:BD是⊙O的切线;
(2)若⊙O的半径为2![]() ,CE=1,试求BD的长.
,CE=1,试求BD的长.
【答案】(1)见解析;(2)4
【解析】
(1)连接OB,由圆的半径相等和已知条件证明∠OBD=90°,即可证明BD是⊙O的切线;
(2)根据三角函数的定义得到![]() ,求得∠A=30°,得到∠DEB=∠AEC=60°,推出△DEB是等边三角形,得到BE=BD,设EF=BF=x,求得AB=2x+2,过O作OH⊥AB于H,解直角三角形即可得到结论.
,求得∠A=30°,得到∠DEB=∠AEC=60°,推出△DEB是等边三角形,得到BE=BD,设EF=BF=x,求得AB=2x+2,过O作OH⊥AB于H,解直角三角形即可得到结论.
(1)证明:连接OB,
∵OB=OA,DE=DB,
∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,
∴∠A+∠AEC=∠A+∠DEB=90°,
∴∠OBA+∠ABD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)解:∵⊙O的半径为![]() ,点C是半径OA的中点,
,点C是半径OA的中点,
∴![]() ,
,
∵CE=1,
∴![]() ,
,
∴∠A=30°,
∵∠ACE=90°,
∴∠DEB=∠AEC=60°,
∵DF垂直平分BE,
∴DE=DB,
∴△DEB是等边三角形,
∴BE=BD,
设EF=BF=x,
∴AB=2x+2,
过O作OH⊥AB于H,
∴AH=BH=x+1,
∵![]() ,
,
∴![]() ,
,
∴AB=6,
∴BD=BE=AB﹣AE=4.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】黄山景区销售一种旅游纪念品,已知每件进价为![]() 元,当销售单价定为
元,当销售单价定为![]() 元时,每天可以销售
元时,每天可以销售![]() 件.市场调查反映:销售单价每提高
件.市场调查反映:销售单价每提高![]() 元,日销量将会减少
元,日销量将会减少![]() 件.物价部门规定:销售单价不低于
件.物价部门规定:销售单价不低于![]() 元,但不能超过
元,但不能超过![]() 元,设该纪念品的销售单价为
元,设该纪念品的销售单价为![]() (元),日销量为
(元),日销量为![]() (件).
(件).
(1)直接写出![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)求日销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)的函数关系式.并求当
(元)的函数关系式.并求当![]() 为何值时,日销售利润最大,最大利润是多少?
为何值时,日销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
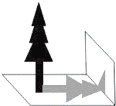
A.4.25mB.4.45mC.4.60mD.4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.

(1)求剩余木料的面积.
(2)如果木工想从剩余的木料中截出长为1.5dm,宽为ldm的长方形木条,最多能截出 块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2﹣4x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.
(1)若点P(﹣1,2)在图象G上,求n的值.
(2)当n=﹣1时.
①若Q(t,1)在图象G上,求t的值.
②当k≤x≤3(k<3)时,图象G对应函数的最大值为5,最小值为﹣5,直接写出k的取值范围.
(3)当以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)为顶点的矩形ABCD的边与图象G有且只有三个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
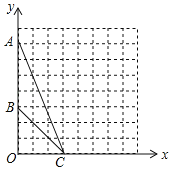
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)在图中作出△ABC的外接圆(利用格图确定圆心);
(2)圆心坐标为 ;外接圆半径r为 ;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A,B(点A在点B的左侧).
(1)当a=﹣1时,求A,B两点的坐标;
(2)过点P(3,0)作垂直于x轴的直线l,交抛物线于点C.
①当a=2时,求PB+PC的值;
②若点B在直线l左侧,且PB+PC≥14,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:t1,t2是方程t2+2t﹣24=0的两个实数根,且t1<t2,抛物线y=![]() x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com