
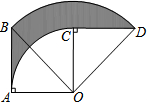
 如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π. 分析 根据旋转的性质得到AO=CO=2,BO=DO=2$\sqrt{2}$,然后根据阴影部分面积=S扇形OBD+S△AOB-S扇形OAC-S△COD=S扇形OBD-S扇形OAC,代入数值即可得到结果.
解答 解:∵Rt△OAB中,∠AOB=45°,AB=2,
∴AO=2,BO=2$\sqrt{2}$,
∵将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,
∴CO=OA=2,DO=OB=2$\sqrt{2}$,
∴阴影部分面积=S扇形OBD+S△AOB-S扇形OAC-S△COD=S扇形OBD-S扇形OAC=$\frac{90•π×(2\sqrt{2})^{2}}{360}$-$\frac{90•π×{2}^{2}}{360}$=π,
故答案为:π.
点评 本题考查了解直角三角形,旋转的性质,扇形的面积公式,熟记扇形的面积公式是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<0<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
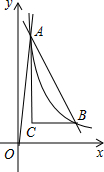 如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.
如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=$\frac{k}{x}$交于点A,点A的横坐标为$\frac{1}{2}$,反比例函数y=$\frac{k}{x}$图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班同学的体重情况 | B. | 了解我省初中学生的兴趣爱好情况 | ||
| C. | 了解一批电灯泡的使用寿命 | D. | 了解我省农民工的年收入情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com