

分析 (1)只需证明△ACD≌△BCE即可.
(2)又等腰三角形的性质及(1)的证明求出∠CED与∠AEB的度数即可.
(3)证明△ABE是直角三角形,并有等腰三角形的性质证明DM=ME=5,然后代值求解即可.
解答 解:(1)如图②,∵∠ACB=∠DCE,
∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE.
又在△ACD与△BCE中,$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠CBE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE(SAS)
∴AD=BE
故答案是:∠CBE; BE
(2)∵CA=CB,
∴∠CAD=∠CBE=70°
∵∠ACD=∠BCE.
∴∠EAB+∠CAE=∠EAB+∠CBE=70°
∴∠EAB+∠ABC+∠CBE=140°,
∴∠AEB=40°
∴∠AEB=70°+40°=110°
故答案是110°
(3)∵CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠CAB+∠CBA=90°,
由(1)知:∠ACD=∠BCE.
∴∠EAB+∠ABE=90°.
∵CD=CE,CM⊥ME,
∴DM=ME=5
∴S△AEB=$\frac{1}{2}$AE•BE=$\frac{1}{2}$×(4+10)×4=28
故答案是28
点评 本题考查了全等三角形的判定与性质、三角形的面积、等边三角形的性质等知识点,解题的关键是能够综合应用以上知识点


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:选择题
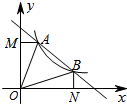 如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )
如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大3倍 | C. | 扩大6倍 | D. | 扩大9倍 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com