
【题目】(1)当![]() 时,求两个代数式
时,求两个代数式![]() 与
与![]() 的值;
的值;
(2)当![]() 时,再求以上两个代数式的值;
时,再求以上两个代数式的值;
(3)你能从上面的计算结果中,发现上面有什么结论?
结论是: ;
【答案】(1)1,1;(2)25,25;(3) (a+b)2= a2+2ab+b2.
【解析】
(1)将a=-2,b=1分别代入两个代数式,求出两个代数式的值;
(2)将a=-2,b=-3分别代入(1)题中的两个代数式,求出两个代数式的值;
(3)观察(1)和(2)的结果,发现(a+b)2= a2+2ab+b2.
解:(1)∵a=-2,b=1,
∴(a+b)2=(-2+1)2=(-1)2=1;
a2+2ab+b2=(-2)2+2×(-2)×1+12=4-4+1=1.
(2)∵a=-2,b=-3,
∴(a+b)2=(-2-3)2=(-5)2=25;
a2+2ab+b2=(-2)2+2×(-2)×(-3)+(-3)2=4+12+9=25.
(3) (a+b)2= a2+2ab+b2
故答案为:(1)1,1;(2)25,25;(3) (a+b)2= a2+2ab+b2.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
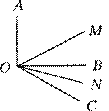
【题目】(1)已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,求∠MON与∠AOB的关系.
(2)如果(1)中,改变∠AOB的大小,其他条件不变,求∠MON与∠AOB的关系.
(3)你从(1),(2)的结果中能发现什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①有理数分为正有理数与负有理数;
②飞机向前运动![]() 千米记作
千米记作![]() 千米,则向下运动
千米,则向下运动![]() 千米记作
千米记作![]() 千米;
千米;
③零既是自然数,又是整数;④![]() 既是负数,又是分数.其中正确的有( )
既是负数,又是分数.其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为⊙O的直径,AB=4.动点P从A点出发,以每秒π个单位的速度在⊙O上按顺时针方向运动一周.设动点P的运动时间为t秒,点C是圆周上一点,且∠AOC=40°,当t=秒时,点P与点C中心对称,且对称中心在直径AB上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.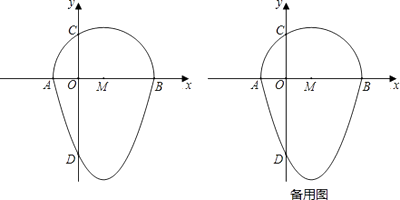
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A , B , C , CD=;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF , 若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 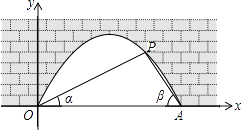
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com