【题目】已知
a2+10b2+
c2﹣4ab＝
a﹣2bc﹣，则a﹣2b+c＝_____．
【答案】-14.
【解析】
首先把已知等式进行变形，再配方得出（3a-2）2+（18b+2c）2+（12a-6b）2=0，得出3a-2=0，18b+2c=0，12a-6b=0，求出a=
，b=
，c=-12，即可得出结果．
a2+10b2+
c2﹣4ab＝
a﹣2bc﹣，
整理得：153a2+360b2+4c2﹣144ab＝12a﹣72bc﹣4，
即（9a2﹣12a+4）+（324b2+72b+4c2）+（144a2﹣144ab+36b2）＝0，
∴（3a﹣2）2+（18b+2c）2+（12a﹣6b）2＝0，
∴3a﹣2＝0，18b+2c＝0，12a﹣6b＝0，
∴a＝，b＝，c＝﹣12，
∴a﹣2b+c＝﹣2×﹣12＝﹣14，
故答案为：﹣14．
科目：初中数学 来源： 题型：
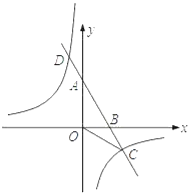
【题目】如图，已知A、B两点的坐标分别为A（0，2
），B（2，0），直线AB与反比例函数y=
的图象交于点C和点D（﹣1，a）．
（1）求直线AB和反比例函数的解析式；
（2）求∠ACO的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知x1、x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根，使得(3x1-x2)(x1-3x2)=-80成立，求其实数a的可能值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校李老师布置了两道解方程的作业题：
选用合适的方法解方程：
（1）x（x+1）=2x；（2）（x+1）（x﹣3）=7
以下是王萌同学的作业：
解：（1）移项，得x（x+1）﹣2x=0 分解因式得，x（x+1﹣2）=0 所以，x=0，或x﹣1=0 所以，x1=0，x2=1 | （2）变形得，（x+1）（x﹣3）=1×7 所以，x+1=7，x﹣3=1 解得，x1=6，x2=4 |
请你帮王萌检查他的作业是否正确，把不正确的改正过来．
查看答案和解析>>
科目：初中数学 来源： 题型：
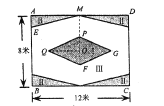
【题目】如图，某校准备给长12米，宽8米的矩形
室内场地进行地面装饰，现将其划分为区域Ⅰ（菱形
），区域Ⅱ（4个全等的直角三角形），剩余空白部分记为区域Ⅲ；点
为矩形和菱形的对称中心，
，
，
，为了美观，要求区域Ⅱ的面积不超过矩形面积的
，若设
米.
甲 | 乙 | 丙 | |
单价（元/米2） |
|
|
|
（1）当
时，求区域Ⅱ的面积.
（2）计划在区域Ⅰ，Ⅱ分别铺设甲，乙两款不同的深色瓷砖，区域Ⅲ铺设丙款白色瓷砖，
①在相同光照条件下，当场地内白色区域的面积越大，室内光线亮度越好.当
为多少时，室内光线亮度最好，并求此时白色区域的面积.
②三种瓷砖的单价列表如下，
均为正整数，若当
米时，购买三款瓷砖的总费用最少，且最少费用为7200元，此时
__________，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程x2－（m＋2）x＋（2m－1）=0。
（1）求证：方程恒有两个不相等的实数根；
（2）若此方程的一个根是1，请求出方程的另一个根，并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为进一步深化基教育课程改革，构建符合素质教育要求的学校课程体系，某学校自主开发了A书法、B阅读，C足球，D器乐四门校本选修课程供学生选择，每门课程被选到的机会均等．
（1）学生小红计划选修两门课程，请写出所有可能的选法；
（2）若学生小明和小刚各计划送修一门课程，则他们两人恰好选修同一门课程的概率为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
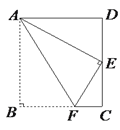
【题目】如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在CD边的中点E处, 折痕为AF，若CD=6，则AF等于__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，点O在对角线BD上，以OD为半径的⊙O与AD、BD分别交于点E、F，且∠ABE=∠DBC.
（1）求证：BE与⊙O相切；
（2）若
，CD=2，求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
