练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．先化简再求值：（2x+3）（2x-3）+（x-2）2-5x（x-1），其中x=4．

    分析 根据平方差公式、完全平方公式、单项式乘多项式可以化简本题，然后将x=4代入化简后的式子即可解答本题．

    解答 解：（2x+3）（2x-3）+（x-2）2-5x（x-1）
    =4x2-9+x2-4x+4-5x2+5x
    =x+5，
    当x=4时，原式=4+5=9．

    点评 本题考查整式的混合运算-化简求值，解题的关键是明确整式的混合运算的计算方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

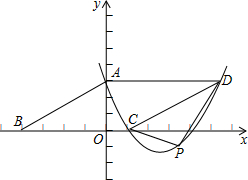    17．如图所示，在平面直角坐标系中，△ABC的顶点坐标分别为点A（0，3）、B（-4，0）、C（1，0），沿AC所在直线将△ABC翻折使点B落在点D处，抛物线y=ax2+bx+c经过A、C、D三点．
    （1）求证：四边形ABCD是菱形；
    （2）求抛物线的解析式；
    （3）在直线CD下方的抛物线上，是否存在一点P，使△PDC的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知：在Rt△ABC中，∠C=90°，BC=3，tanB=$\sqrt{3}$．试求AB的长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如果y=$\sqrt{2x-16}$+$\sqrt{8-x}$+16，那么$\frac{x+y}{\sqrt{2x}}$+$\frac{x-y}{\sqrt{y}}$的值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，直线y=ax+b（a、b为常数，且a≠0）与反比例函数y=$\frac{k}{x}$（k为常数，且k≠0）的图象交于点A（-2，4），点B（-4，n），与x轴交于点C；
    （1）试确定反比例函数的解析式及n的值；
    （2）求△AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，羊年春节到了，小明亲手制作了3张一样的卡片，在每张卡片上分别写上“新”“年”“好”三个字，并随机放入一个不透明的信封中，然后让小芳分三次从信封中摸3张卡片（每次摸1张，摸出不放回）．
    （1）小芳第一次抽取的卡片是“新”字的概率是多少？
    （2）请通过画树状图或列表，求小芳先后抽取的3张卡片分别是“新年好”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，AB为⊙O的直径，动点P从点A开始，沿边AD向点D以1cm/s的速度运动，点Q从点C开始，沿边CB向点B以3cm/s的速度运动，点P、Q分别从点A、C出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．
    （1）当t为何值时，四边形PQCD是平行四边形？
    （2）当t为何值时，直线PQ与⊙O相切、相交、相离？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在△ABC中，AD、AE分别是高和角的平分线，∠B=70°，∠C=40°，求∠DAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在△ABC与△DCE中，已知∠ACB=90°，∠DCE=90°，且DC⊥AB，DC、DE分别交AB于M、N两点，当$\frac{DN}{BC}$=$\frac{MN}{CM}$，DE=10时，求CF的长．

    查看答案和解析>>

    同步练习册答案