
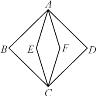
【题目】定义:如图,若菱形AECF与正方形ABCD两个顶点A,C重合,另外两个顶点E,F在正方形ABCD的内部,则称菱形AECF为正方形ABCD的内含菱形.
若正方形的周长为16,其内含菱形边长是整数,则内含菱形的周长为________;
若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为________.
【答案】12 ![]()
【解析】
连接AC,BD,AC、BD交于点O,如图,由正方形和菱形的性质可得E、F在BD上,且EF⊥AC,易求得OA的长,在Rt△AOE中,由勾股定理可得OA2+OE2=AE2,由![]() 可得
可得![]() ,然后即可确定整数AE的长,进而可得菱形的周长;由正方形的面积是18可求出其边长,进而可求得AC的长,然后即可求出OE的长,进一步根据勾股定理即可求出菱形的边长.
,然后即可确定整数AE的长,进而可得菱形的周长;由正方形的面积是18可求出其边长,进而可求得AC的长,然后即可求出OE的长,进一步根据勾股定理即可求出菱形的边长.
解:连接AC,BD,AC、BD交于点O,如图,
∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,
∵四边形AECF是菱形,∴E、F在BD上,且EF⊥AC,
∵正方形的周长为16,∴AB=4,
∴2OA2=AB2,即2OA2=16,解得:OA=2![]() ,
,
∴OE<2![]() ,
,
在Rt△AOE中,∵OA2+OE2=AE2,∴8+OE2=AE2,
∵![]() ,∴
,∴![]() ,
,
∵AE是整数,∴AE=3,则内含菱形的周长为12;

若正方形的面积为18,∴AB=3![]() ,
,
∴OA=3,
∵其内含菱形的面积为6,
∴EF=2,∴OE=1,
则内含菱形的边长![]() .
.
故答案为:12;![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
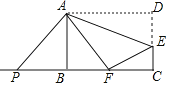
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.在对这些数据整理后,绘制了如图的统计图表:
睡眠时间分组统计表:
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |
请根据以上信息,解答下列问题:
(1)m= ,n= ,a= ,b= ;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在 组(填组别);在扇形统计图中,第4组所在扇形的圆心角是 度;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h.请估计该校学生中睡眠时间符合要求的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
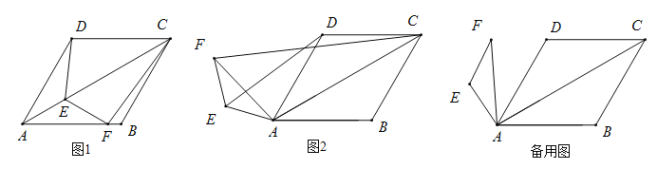
【题目】如图1,在菱形ABCD中,![]() ,点E,F分别是AC,AB上的点,且
,点E,F分别是AC,AB上的点,且![]() ,猜想:
,猜想:
①![]() 的值是_______;
的值是_______;
②直线DE与直线CF所成的角中较小的角的度数是_______.
(2)类比探究:如图2,将绕![]() 点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
点A逆时针旋转,在旋转的过程中,(1)中结论是否成立,就图2的情形说明理由.
(3)拓展延伸:
在![]() 绕点A旋转的过程中,当
绕点A旋转的过程中,当![]() 三点共线时,请直接写出CF的长.
三点共线时,请直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式![]() 的几何意义是数轴上
的几何意义是数轴上![]() 所对应的点与2所对应的点之间的距离;因为
所对应的点与2所对应的点之间的距离;因为![]() ,所以
,所以![]() 的几何意义就是数轴上
的几何意义就是数轴上![]() 所对应的点与
所对应的点与![]() 所对应的点之间的距离.
所对应的点之间的距离.
⑴. 发现问题:代数式![]() 的最小值是多少?
的最小值是多少?
⑵. 探究问题:如图,点![]() 分别表示的是
分别表示的是![]() ,
,![]() .
.
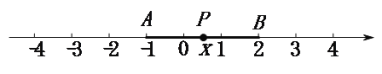
∵![]() 的几何意义是线段
的几何意义是线段![]() 与
与![]() 的长度之和
的长度之和
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() ;当点点
;当点点![]() 在点
在点![]() 的左侧或点
的左侧或点![]() 的右侧时
的右侧时 ![]()
∴![]() 的最小值是3.
的最小值是3.
⑶.解决问题:
①.![]() 的最小值是 ;
的最小值是 ;
②.利用上述思想方法解不等式:![]()
![]()
③.当![]() 为何值时,代数式
为何值时,代数式![]() 的最小值是2.
的最小值是2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中数学 来源: 题型:
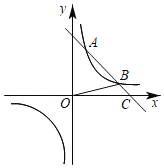
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+b的图象与反比例函数![]() (k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(k>0)的图象相交于A,B两点,与x轴相交于点C(4,0),且点B(3,n),连接OB.
(1)求一次函数和反比例函数的表达式;
(2)求△BOC的面积;
(3)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了![]() :篮球,
:篮球,![]() :毯球,
:毯球,![]() :跳绳,
:跳绳,![]() :健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在
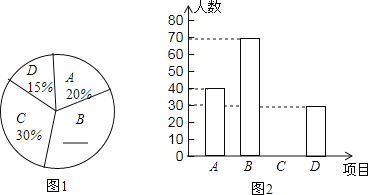
:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在![]() 种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)
种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)
(1)这次调查中,一共调查了 名学生:
(2)请补全两幅统计图:
(3)若由![]() 名最喜欢毯球运动的学生,
名最喜欢毯球运动的学生,![]() 名最喜欢跳绳运动的学生组队外出参加一次联谊活动,欲从中选出
名最喜欢跳绳运动的学生组队外出参加一次联谊活动,欲从中选出![]() 人担任组长(不分正副),求
人担任组长(不分正副),求![]() 人均是最喜欢键球运动的学生的概率
人均是最喜欢键球运动的学生的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 380 | 940 |
餐椅 |
| 160 |
已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同.
(1)求表中a的值;
(2)该商场计划购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.若将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售,请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com