【题目】从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．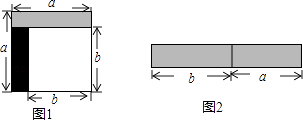 
（1）上述操作能验证的等式是（填A或B）
A.a2﹣2ab+b2=（a﹣b）2
B.a2﹣b2=（a+b）（a﹣b）
（2）应用你从（1）中选出的等式，计算： （1﹣ 
）（1﹣ 
）（1﹣ 
）…（1﹣ 
）（1﹣ 
）．
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】（本题满分12分）已知：点E为AB边上的一个动点.
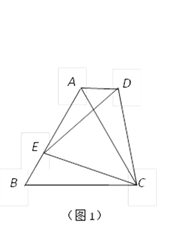
（1）如图1，若△ABC是等边三角形，以CE为边在BC的同侧作等边△DEC ，连结AD.试比较∠DAC与∠B的大小，并说明理由；
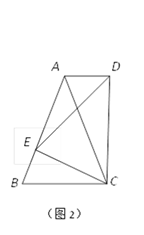
（2）如图2，若△ABC中，AB=AC，以CE为底边在BC的同侧作等腰△DEC ，且
△DEC∽△ABC，连结AD.试判断AD与BC的位置关系，并说明理由；
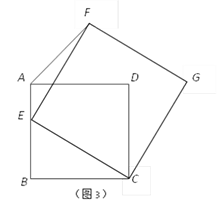
（3）如图3，若四边形ABCD是边长为2的正方形，以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上；
②当点E在AB边上由点B运动至点A时，点F随之运动，求点F的运动路径长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动.
小亮用12根火柴棒，摆成如图所示的“整数三角形”；
小颖分别用24根和30根火柴棒摆出直角“整数三角形”；
小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”.
⑴请你画出小颖和小辉摆出的“整数三角形”的示意图；
⑵你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由.
①画出等边“整数三角形”；
②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
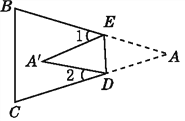
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)?
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
查看答案和解析>>
科目：初中数学 来源： 题型：
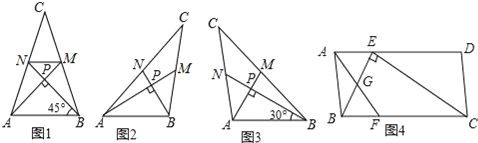
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
【特例探究】
（1）如图1，当tan∠PAB=1，c=4
时，a= ，b= ；
如图2，当∠PAB=30°，c=2时，a= ，b= ；
【归纳证明】
（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
【拓展证明】
（3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3
，AB=3，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）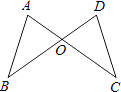 
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】婷婷在计算一个二项式的平方时，得到的正确结果是9x2+24xy+■，但最后一项不慎被污染了，这一项应是（ ）
A.16y2B.8y2C.4y2D.±16y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
