
 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:分析 (1)由图象即可得解;
(2)可根据图中给出的信息,用待定系数法分别求出轮船与快艇的函数关系式.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
解答 解:(1)根据图象,轮船比快艇早出发2小时,
故答案为2;
(2)设表示轮船行驶过程的函数式为y=kx.由图象知:
当x=8时,y=160.
∴8k=160,解得:k=20.
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴$\left\{\begin{array}{l}{2a+b=0}\\{6a+b=160}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=40}\\{b=-80}\end{array}\right.$.
因此表示快艇行驶过程的函数解析式为y=40x-80;
(3)设轮船出发x小时后快艇追上轮船.
20x=40x-80,
x=4,
则x-2=2.
答:快艇出发2小时后赶上轮船.
点评 本题考查了一次函数的图象的运用,行程问题的数量关系的运用,解答时分析清楚函数图象提供的信息是关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
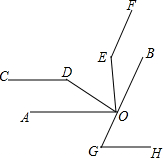 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11x-1 | B. | 11x-10 | C. | 11x+1 | D. | 11x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=$\frac{1}{2}$n(n+1) | B. | m=$\frac{1}{2}$n(n-1) | C. | m=$\frac{1}{2}$n2 | D. | m=n(n-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com