
【题目】如图,一次函数y=﹣![]() x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,△NAB的面积有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.

【答案】(1) y=﹣x2+![]() x+2 (2)4 (3)(0,6),(0,﹣2)或(4,4)
x+2 (2)4 (3)(0,6),(0,﹣2)或(4,4)
【解析】试题分析:(1)首先求得A、B点的坐标,然后利用待定系数法求抛物线的解析式;
(2)本问要点是求得线段MN的表达式,这个表达式是关于t的二次函数,利用二次函数的极值求线段MN的最大值;
(3)本问要点是明确D点的可能位置有三种情形,如答图2所示,不要遗漏.其中D1、D2在y轴上,利用线段数量关系容易求得坐标;D3点在第一象限,是直线D1N和D2M的交点,利用直线解析式求得交点坐标.
试题解析:(1)∵y=﹣![]() +2分别交y轴、x轴于A、B两点,
+2分别交y轴、x轴于A、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=﹣x2+bx+c得c=2,
将x=4,y=0代入y=﹣x2+bx+c得0=﹣16+4b+2,解得b=![]() ,
,
∴抛物线解析式为:y=﹣x2+![]() x+2;
x+2;
(2)如图1,设MN交x轴于点E,
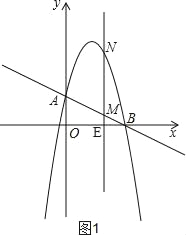
则E(t,0),BE=4﹣t.
∵tan∠ABO=![]() =
=![]() ,
,
∴ME=BEtan∠ABO=(4﹣t)×![]() =2﹣
=2﹣![]() t.
t.
又N点在抛物线上,且xN=t,∴yN=﹣t2+![]() t+2,
t+2,
∴MN=yN﹣ME=﹣t2+![]() t+2﹣(2﹣
t+2﹣(2﹣![]() t)=﹣t2+4t
t)=﹣t2+4t
∴当t=2时,MN有最大值4;
(3)由(2)可知,A(0,2),M(2,1),N(2,5).
以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,
如图2所示.
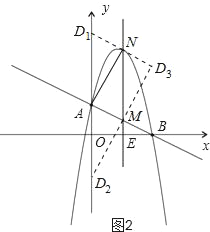
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a﹣2|=4,解得a1=6,a2=﹣2
从而D为(0,6)或D(0,﹣2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
易得D1N的方程为y=﹣![]() x+6,D2M的方程为y=
x+6,D2M的方程为y=![]() x﹣2,
x﹣2,
由两方程联立解得D为(4,4)
故所求的D点坐标为(0,6),(0,﹣2)或(4,4).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】我县某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价贵12元,用12000元购进的科普书本数是用9000元购进的文学书本数的![]() .那么文学书和科普书的单价各是多少元?
.那么文学书和科普书的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东莞市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程 | 收费标准 |
不超出 | 起步价8元 |
超出 | 2.6元/ |
(1)若行驶路程为![]() ,则打车费用为______元;
,则打车费用为______元;
(2)若行驶路程为![]() ,则打车费用为______元(用含
,则打车费用为______元(用含![]() 的代数式表示);
的代数式表示);
(3)某同学周末放学回家,已知打车费用为34元,则他家离学校多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为 .
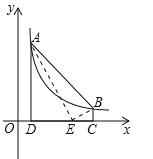
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
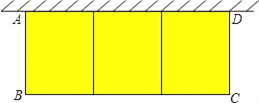
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是边BC上的中线,AE∥BC,DE∥AB,DE与AC交于点O,连接CE.
(1)求证:AD=EC;
(2)若∠BAC=90°,求证:四边形ADCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数![]() ,B点示数
,B点示数![]() ,C点表示数
,C点表示数![]() ,
,![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() =__________,
=__________,![]() =__________,
=__________,![]() =__________;
=__________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设![]() 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求![]() 的值;
的值;
(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,![]() BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com