抛物线y=(x+m)(x-4)与x轴的一个交点为点A,与y轴的交点为点B,其中m>0,且△OAB的面积为4,O为原点,求过A,B两点的一次函数的解析式.
分析:根据抛物线的解析式,可以确定抛物线与x轴的交点以及B点的坐标,进而根据△OAB的面积求出m的值,即可确定A、B的坐标,然后用待定系数法求出直线AB的解析式.(需要注意的是抛物线与x轴的两个交点都有可能是A点,需要分类讨论)
解答:解:令抛物线的y=0,则有(x+m)(x-4)=0,得x=-m,x=4;
∴抛物线与x轴的交点为(-m,0),(4,0);
抛物线的解析式可化为:y=x
2+(m-4)x-4m,则B(0,-4m);
①当A点坐标为(-m,0)时,OA=m,OB=4m;
S
△OAB=
OA•OB=2m
2=4,
解得m=
(负值舍去);
∴A(-
,0),B(0,-4
);
设直线AB的解析式为:y=kx+b,则有:
,
解得
;
∴直线AB的解析式为y=-4x-4
;
②当A点坐标为(4,0)时,OA=4,OB=4m;
S
△OAB=
OA•OB=4m=4,
解得m=1;
∴A(4,0),B(0,-4);
同①可求得直线AB的解析式为y=
x-2;
∴直线AB的解析式为y=-4x-4
或y=
x-2.
点评:此题主要考查了一次函数解析式的确定及三角形面积的求法,同时还考查了分类讨论的数学思想,难度适中.



 A和C,和x轴的另一个交点为B.
A和C,和x轴的另一个交点为B.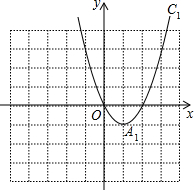 已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.
已知抛物线C1:y=x2-2x的图象如图所示,把C1的图象沿y轴翻折,得到抛物线C2的图象,抛物线C1与抛物线C2的图象合称图象C3.