
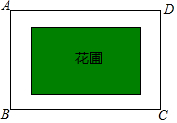
 如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.科目:初中数学 来源: 题型:解答题
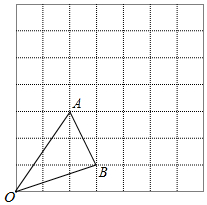 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
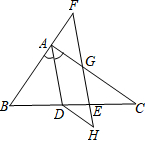 如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.
如图,AD平分∠BAC,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA=180°-∠CEG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知Rt△ABC是直角边长为l的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…依此类推.
如图,已知Rt△ABC是直角边长为l的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…依此类推.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com