
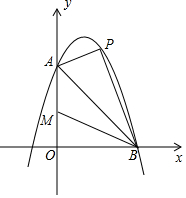
 ��ͼ����֪������y=ax2+2x+c��y�ύ�ڵ�A��0��6������x�ύ�ڵ�B��6��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��ͼ����֪������y=ax2+2x+c��y�ύ�ڵ�A��0��6������x�ύ�ڵ�B��6��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮���� ��1����A��B���꣬���ô���ϵ��������������ߵı���ʽ����Ϊ����ʽ����ö������ꣻ
��2����P��PC��y���ڵ�C������������á�PAC=60�㣬����AC=m����Rt��PAC�У��ɱ�ʾ��PC�ij����Ӷ�����m��ʾ��P�����꣬���������߽���ʽ�����m��ֵ���������P�����ꣻ
��3����t�ɱ�ʾ��P��M�����꣬��P��PE��x���ڵ�E����AB�ڵ�F����ɱ�ʾ��F�����꣬�Ӷ�����t��ʾ��PF�ij����Ӷ��ɱ�ʾ����PAB�����������S�ı���PAMB=S��PAB+S��AMB���ɵõ�S����t�Ķ��κ��������ö��κ��������ʿ���������ֵ��
��� �⣺
��1���������⣬��A��0��6����B��6��0�����������߽���ʽ�ɵ�$\left\{\begin{array}{l}{c=6}\\{36a+12+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=6}\end{array}\right.$��
�������ߵı���ʽΪy=-$\frac{1}{2}$x2+2x+6��
��y=-$\frac{1}{2}$x2+2x+6=-$\frac{1}{2}$��x-2��2+8��
�������ߵĶ�������Ϊ��2��8����
��2����ͼ1����P��PC��y���ڵ�C��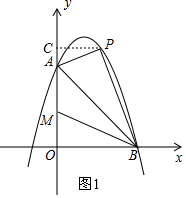
��OA=OB=6��
���OAB=45�㣬
�൱��PAB=75��ʱ����PAC=60�㣬
��tan��PAC=$\frac{PC}{AC}$����$\frac{PC}{AC}$=$\sqrt{3}$��
��AC=m����PC=$\sqrt{3}$m��
��P��$\sqrt{3}$m��6+m����
��P��������������߱���ʽ�ɵ�6+m=-$\frac{1}{2}$��$\sqrt{3}$m��2+2$\sqrt{3}$m+6�����m=0��m=$\frac{4}{3}$$\sqrt{3}$-$\frac{2}{3}$��
�����飬P��0��6�����A�غϣ��������⣬��ȥ��
�������P��������4-$\frac{2}{3}$$\sqrt{3}$��$\frac{16}{3}$+$\frac{4}{3}$$\sqrt{3}$����
��3�������������ƶ�t��ʱ����P��t��-$\frac{1}{2}$t2+2t+6����M��0��6-t����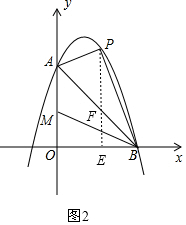
��ͼ2����PE��x���ڵ�E����AB�ڵ�F����EF=EB=6-t��
��F��t��6-t����
��FP=$\frac{1}{2}$t2+2t+6-��6-t��=-$\frac{1}{2}$t2+3t��
�ߵ�A��PE�ľ�����OE����B��PE�ľ������BE��
��S��PAB=$\frac{1}{2}$FP•OE+$\frac{1}{2}$FP•BE=$\frac{1}{2}$FP•��OE+BE��=$\frac{1}{2}$FP•OB=$\frac{1}{2}$����-$\frac{1}{2}$t2+3t����6=-$\frac{3}{2}$t2+9t����S��AMB=$\frac{1}{2}$AM•OB=$\frac{1}{2}$��t��6=3t��
��S=S�ı���PAMB=S��PAB+S��AMB=-$\frac{3}{2}$t2+12t=-$\frac{3}{2}$��t-4��2+24��
�൱t=4ʱ��S�����ֵ�����ֵΪ24��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ֱ�������ε����ʡ����κ��������ʡ������ε����������˼���֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2���й���Rt��PAC�ǽ���Ĺؼ����ڣ�3������t��ʾ��P��M�����꣬��ʾ��PF�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
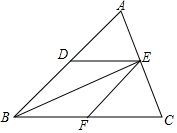 ��ͼ����ABC�У�DE��BC��EF��AB��Ҫ�ж��ı���DBFE�����Σ�����Ҫ���ӵ������ǣ�������
��ͼ����ABC�У�DE��BC��EF��AB��Ҫ�ж��ı���DBFE�����Σ�����Ҫ���ӵ������ǣ�������| A�� | AB=AC | B�� | AD=BD | C�� | BE��AC | D�� | BEƽ�֡�ABC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���䣨�꣩ | 12 | 13 | 14 | 15 |
| ���������� | 2 | 4 | 3 | 1 |
| A�� | 12 | B�� | 13 | C�� | 13.5 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 95 | B�� | 90 | C�� | 85 | D�� | 80 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3b6 | B�� | -a3b6 | C�� | ab6 | D�� | -ab6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com