Question

9．如图，在平面直角坐标系中，△AOB为等腰直角三角形，A（2$\sqrt{2}$，2$\sqrt{2}$）
（1）求B点坐标．
（2）点A关于y轴的对称点为点D，点P从点D出发沿射线DO运动，速度为每秒钟2个单位长度，连接AP，若△AOP的面积为S，请用含有t的式子表示S，并直接写出t的取值范围．
（3）过点A作AE⊥y轴于E，F为x轴负半轴上一点，G在EF延长线上，以EG为直角边作等腰Rt△EGH，AM∥y轴交EH于M，
连接FM，求证：AM=OF+FM．

Answer 1

分析 （1）根据△AOB为等腰直角三角形，作AE⊥OB于E，根据AE和OE的长，可得B点坐标；
（2）先作点A关于y轴的对称点D，连接DO并延长，分两种情况进行讨论：点P在线段DO上运动；点P在DO的延长线上运动，分别根据△AOP的面积=$\frac{1}{2}$×PO×AO，求得S关于t的表达式；
（3）先在AM上截取AN=OF，连EN，易证△EAN≌△EOF，再根据角与角之间的关系，证明△NEM≌△FEM，则有AM-MF=OF，即可得出等式成立．

解答 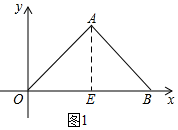解：（1）如图1，作AE⊥OB于E，
∵A（2$\sqrt{2}$，2$\sqrt{2}$），
∴OE=2$\sqrt{2}$，
∵△AOB为等腰直角三角形，且AE⊥OB，
∴OE=EB=2$\sqrt{2}$，
∴OB=4$\sqrt{2}$，
∴B（4$\sqrt{2}$，0）；

（2）作点A关于y轴的对称点D，连接DO并延长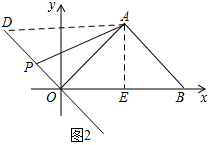，则AO=DO，
∵Rt△AOE中，AE=OE=2$\sqrt{2}$，
∴AO=$\sqrt{A{E}^{2}+O{E}^{2}}$=4，∠AOE=45°，
∴DO=4，∠AOD=90°，
∵点P从点D出发沿射线DO运动，速度为每秒钟2个单位长度，
∴DP=2t，
如图2，当点P在线段DO上运动时，PO=4-2t，
∵△AOP的面积=$\frac{1}{2}$×PO×AO，
∴S=$\frac{1}{2}$（4-2t）×4=8-4t（0≤t＜2）；
如图3，当点P在DO的延长线上运动时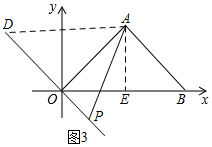，PO=2t-4，
∵△AOP的面积=$\frac{1}{2}$×PO×AO，
∴S=$\frac{1}{2}$（2t-4）×4=4t-8（t≥2），
综上所述，S=$\left\{\begin{array}{l}{8-4t（0≤t＜2）}\\{4t-8（t≥2）}\end{array}\right.$；

（3）如图4，在AM上截取AN=OF，连EN．
∵A（2$\sqrt{2}$，2$\sqrt{2}$），
∴AE=OE=2$\sqrt{2}$，
又∵∠EAN=∠EOF=90°，AN=OF，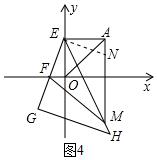
∴△EAN≌△EOF（SAS），
∴∠OEF=∠AEN，EF=EN，
又∵△EGH为等腰直角三角形，
∴∠GEH=45°，即∠OEF+∠OEM=45°，
∴∠AEN+∠OEM=45°
又∵∠AEO=90°，
∴∠NEM=45°=∠FEM，
又∵EM=EM，
∴△NEM≌△FEM（SAS），
∴MN=MF，
∴AM-MF=AM-MN=AN，
∴AM-MF=OF，
即AM=OF+FM．

点评 此题是几何变换综合题，考查了全等三角形的判定与性质、等腰直角三角形的性质，轴对称的性质，勾股定理以及三角形的面积计算等知识的综合应用，考查学生综合运用数学知识的能力．解决问题的关键是作辅助线构造等腰直角三角形和全等三角形，解题时注意分类思想的运用．