

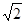 ;②
;②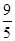 或
或 ;(2)△CEF与△ABC相似.理由详见解析.
;(2)△CEF与△ABC相似.理由详见解析.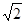 .②分两种情况:一、当△CEF∽△CAB时,如图2,则有∠CEF=∠CAB,所以EF∥AB,根据题意,点C与点D关于直线EF对称,所以CD⊥EF,所以CD⊥AB,由三角形的面积公式可求得CD=2.4,在△ACD中,由勾股定理可得AD=
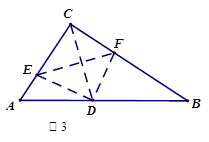
.②分两种情况:一、当△CEF∽△CAB时,如图2,则有∠CEF=∠CAB,所以EF∥AB,根据题意,点C与点D关于直线EF对称,所以CD⊥EF,所以CD⊥AB,由三角形的面积公式可求得CD=2.4,在△ACD中,由勾股定理可得AD=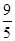 ;二、当△CFE∽△CAB时,如图3,此时有∠A=∠CFE, ∠B=∠CEF,又∠A+∠B=90°,所以∠A+∠CEF="90°," ∠B+∠CFE=90°,前面已证EF⊥CD,所以∠DCE+∠CEF=90°,∠DCF+∠CFE=90°,所以∠A=∠ACD, ∠B=∠BCD,所以AD=CD=BD=2.5;(2)利用折叠前后对应的部分关于折叠线对称,以及直角三角形斜边上的中线等于斜边的一半,即可求得∠A=∠CFE, ∠B=∠CEF,所以得证.
;二、当△CFE∽△CAB时,如图3,此时有∠A=∠CFE, ∠B=∠CEF,又∠A+∠B=90°,所以∠A+∠CEF="90°," ∠B+∠CFE=90°,前面已证EF⊥CD,所以∠DCE+∠CEF=90°,∠DCF+∠CFE=90°,所以∠A=∠ACD, ∠B=∠BCD,所以AD=CD=BD=2.5;(2)利用折叠前后对应的部分关于折叠线对称,以及直角三角形斜边上的中线等于斜边的一半,即可求得∠A=∠CFE, ∠B=∠CEF,所以得证.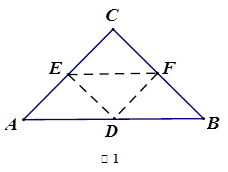

 ;②
;②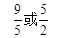 ;
;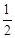 AB,∴∠DCB=∠B.
AB,∴∠DCB=∠B.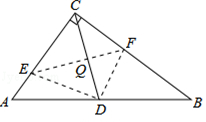


科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的值 .
的值 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题


 =DM·EN
=DM·EN查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com