
| |a-1| |
| a2+2a-3 |
| 1 |
| a+3 |
| A、小明 | B、小华 |
| C、小颖 | D、都有道理 |
| |a-1| |
| a2+2a-3 |
| |a-1| |
| (a+3)(a-1) |
| |a-1| |
| a2+2a-3 |
| 1 |
| a+3 |
| |a-1| |
| (a+3)(a-1) |
| a-1 |
| (a+3)(a-1) |
| 1 |
| a+3 |
|
| |a-1| |
| a2+2a-3 |
| 1 |
| a+3 |


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:044
为了了解你所在地区老年人的健康状况,你准备怎样收集数据?下面分别是小明、小颖、小华三位同学的调查结果.
小明:我调查了10名老年邻居,他们一年生病的次数如图所示.

小华:我在医院调查了1000名老年人,他们一年中生病的次数如图所示.

小颖:我在公园里调查了1000名老年人,他们一年中生病的次数如下表所示:

(1)你同意他们的做法吗?说说你的理由;
(2)为了了解该地区老年人的健康状况,你认为应当怎样调查?与你的同伴交流.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
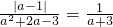 成立.
成立.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| |a-1| |
| a2+2a-3 |
| 1 |
| a+3 |
| A.小明 | B.小华 | C.小颖 | D.都有道理 |
查看答案和解析>>
科目:初中数学 来源:同步题 题型:单选题
 成立.
成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com