
【题目】如图,抛物线y=ax2﹣![]() x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
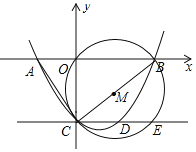
(1)求该抛物线的解析式;
(2)当△PDE是以DE为底边的等腰三角形时,求点P的坐标;
(3)当四边形ACPB的面积最大时,求点P的坐标并求出最大值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)P(3,﹣
x﹣3;(2)P(3,﹣![]() );(3)点P(2,﹣3),最大值为12
);(3)点P(2,﹣3),最大值为12
【解析】
(1)用交点式设出抛物线的表达式,化为一般形式,根据系数之间的对应关系即可求解;
(2)根据(1)中的表达式求出点C(0,-3),函数对称轴为:x=1,则点D(2,-3),点E(4,-3),当△PDE是以DE为底边的等腰三角形时,点P在线段DE的中垂线上,据此即可求解;
(3)求出直线BC的表达式,设出P、H点的坐标,根据四边形ACPB的面积=S△ABC+S△BHP+S△CHP进行计算,化为顶点式即可求解.
(1)抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
即﹣2a=﹣![]() ,解得:a=
,解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)当x=0时,y=-3,故点C的坐标为(0,﹣3),
函数对称轴为:x=![]() =1,
=1,
∵CE∥AB
∴点D(2,﹣3),点E(4,﹣3),
则DE的中垂线为:x=![]() =3,
=3,
当x=3时,y=![]() x2﹣
x2﹣![]() x﹣3=﹣
x﹣3=﹣![]() ,
,
故点P(3,﹣![]() );
);
(3)设直线BC的解析式为y=kx+b,
把B(4,0)C(0,﹣3)代入得:![]()
解得: 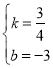
∴直线BC的表达式为:y=![]() x﹣3,
x﹣3,
故点P作y轴的平行线交BC于点H,
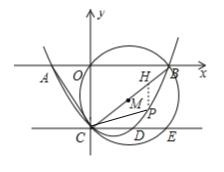
设点P(x,![]() x2﹣
x2﹣![]() x﹣3),则点H(x,
x﹣3),则点H(x,![]() x﹣3);
x﹣3);
四边形ACPB的面积=S△ABC+S△BHP+S△CHP=![]() 3×6+
3×6+![]() HP×OB=9+
HP×OB=9+![]() ×4×(
×4×(![]() x﹣3﹣
x﹣3﹣![]() x2+
x2+![]() x+3)=﹣
x+3)=﹣![]() x2+3x+9=
x2+3x+9=![]() ,
,
∵﹣![]() <0,故四边形ACPB的面积有最大值为12,此时,点P(2,﹣3).
<0,故四边形ACPB的面积有最大值为12,此时,点P(2,﹣3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家![]() 他60岁时完成的
他60岁时完成的![]() 直指算法统宗
直指算法统宗![]() 是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法
是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法![]() 对书中某一问题改编如下:
对书中某一问题改编如下:
一百馒头一百僧,大僧三个更无争;
小僧三人分一个,大僧共得几馒头.
一百馒头一百僧,大僧三个更无争;
小僧三人分一个,大僧共得几馒头.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个正好分完,大和尚共分得![]()
![]() 个馒头
个馒头
A. 25B. 72C. 75D. 90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
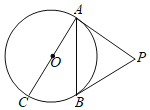
(1)求∠BAC的度数;
(2)若PA=![]() ,求点O到弦AB的距离.
,求点O到弦AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
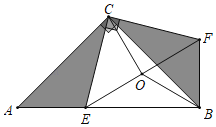
【题目】如图,等腰Rt△ABC,AB=6,点E是斜边AB上的一点(端点A、B除外),将△CAE绕C逆时针旋转90°至△CBF,连接EF,且EF的中点为O,连OB、OC,设AE=x,
(1)求证:OB=OC;
(2)用x表示△BEF的面积S△BEF,并求S△BEF的最大值;
(3)用x表示四边形BECF的周长C,并求C的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
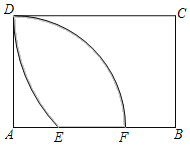
【题目】如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=![]() ,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020比佛利”无锡马拉松赛将于3月22日鸣枪开跑,本次比赛设三个项目:A.全程马拉松;B.半程马拉松;C.迷你马拉松.小明和小红都报名参与该赛事的志愿者服务工作,若两人都已被选中,届时组委会随机将他们分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请利用树状图或列表法求两人被分配到同一个项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
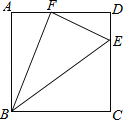
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=![]() ,则tan∠EBC的值为( )
,则tan∠EBC的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]()
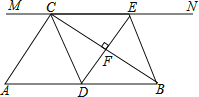
(1)当![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(2)当![]() 为
为![]() 中点时,
中点时,![]() 等于 度时,四边形
等于 度时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com