Question

1．如图1，△ADL内接于⊙O，AB是△ADL的高，连接AO．
（1）求证：∠DAO=∠BAL；
（2）如图2，DC为△ADL的高，交AB于点E，∠DAL=60°，求证：AE=AO；
（3）如图3，在（2）的条件下，连接OE，若AD-AL=$\sqrt{3}$，△AOE的面积为$\frac{5}{4}$$\sqrt{3}$，求DL的长．

Answer 1

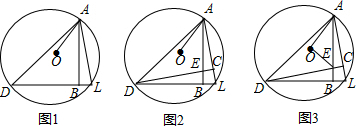
分析 （1）如图1中，延长AO交⊙O于F，连接DF．由∠DAO+∠F=90°，∠BAL+∠L=90°，因为∠F=∠L，根据等角的余角相等即可证明．
（2）如图2中，作OG⊥AD于G．只要证明△AOG≌△AEC，即可解决问题．
（3）如图3中，延长LE交AD于I，连接LO，延长LO交⊙O于G，作AJ⊥OE于J，在AD上取一点H，使得AH=AL，连接LH、DG、OH．只要证明四边形DHEO是等腰梯形，推出DH=OE，由AD-AL=DH=$\sqrt{3}$，推出DH=OE=$\sqrt{3}$，由S_△AOE=$\frac{1}{2}$•OE•AJ=$\frac{5}{4}$$\sqrt{3}$，推出AJ=$\frac{5}{2}$，推出OJ=JE=$\frac{\sqrt{3}}{2}$，在Rt△AOJ中，OA=$\sqrt{A{J}^{2}+O{J}^{2}}$=$\sqrt{7}$，推出GL=2OA=2$\sqrt{7}$，在Rt△DGL中，根据∠GLD=30°，GL=2$\sqrt{7}$，即可解决问题．

解答 （1）证明：如图1中，延长AO交⊙O于F，连接DF．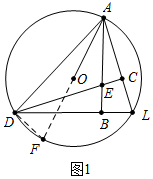

∵AD是直径，
∴∠ADF=90°，
∵AB⊥DL，
∴∠ABL=90°，
∴∠DAO+∠F=90°，∠BAL+∠L=90°，
∵∠F=∠L，
∴∠DAO=∠BAL．

（2）证明：如图2中，作OG⊥AD于G．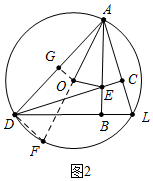

∵∠DAL=60°，∠DCA=90°，
∴∠ADC=30°，
∴AC=$\frac{1}{2}$AD，
∵OG⊥AD，
∴AG=$\frac{1}{2}$AD，
∴AG=AC，
在△AOG和△AEC中，
$\left\{\begin{array}{l}{∠OAG=∠EAC}\\{AG=AC}\\{∠AGO=∠ACE}\end{array}\right.$，
∴△AOG≌△AEC，
∴AO=AE．

（3）解：如图3中，延长LE交AD于I，连接LO，延长LO交⊙O于G，作AJ⊥OE于J，在AD上取一点H，使得AH=AL，连接LH、DG、OH．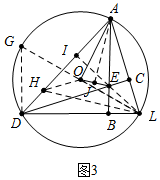

∵AB、DC是△ADL的高，
∴CI⊥AD，
∵AH=AL，∠HAL=60°，
∴△AHL是等边三角形，
∴∠ALI=∠ILD=30°，
∵AH=AL，∠HAO=∠LAE，AO=AE，
∴△AHO≌△ALE，
∴OH=EL，∠AHO=∠ALE=∠OHL=30°，
∵OA=AE，AJ⊥OE，
∴∠JAO=∠JAE，
∴∠JAH=∠JAL，∵AH=AL，
∴AJ⊥HL，
∴OE∥HL，
∴∠HOE=180°-∠OHL=150°，∠DHO=150°，
∴∠DHO=∠HOE，
∵∠AHO=∠ADC=30°，
∴HO∥DC，
∴四边形DHEO是等腰梯形，
∴DH=OE，
∵AD-AL=DH=$\sqrt{3}$，
∴DH=OE=$\sqrt{3}$，
∵S_△AOE=$\frac{1}{2}$•OE•AJ=$\frac{5}{4}$$\sqrt{3}$，
∴AJ=$\frac{5}{2}$，
∴OJ=JE=$\frac{\sqrt{3}}{2}$，
在Rt△AOJ中，OA=$\sqrt{A{J}^{2}+O{J}^{2}}$=$\sqrt{7}$，
∴GL=2OA=2$\sqrt{7}$，
∵∠G=∠DAL=60°，
∵GL是直径，
∴∠GDL=90°，
在Rt△DGL中，∵∠GLD=30°，GL=2$\sqrt{7}$，
∴DG=$\frac{1}{2}$GL=$\sqrt{7}$，
∴DL=$\sqrt{3}$DG=$\sqrt{21}$．

点评 本题考查圆综合题、全等三角形的判定和性质、等边三角形的判定和性质、等腰梯形的判定和性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，本题的突破点是证明四边形DHEO是等腰梯形，推出OE=DH=$\sqrt{3}$，本题比较难，属于中考压轴题．