
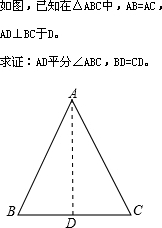
 小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).
小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).
|
|


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:044
小明对小华说:“我在证明‘等腰三角形两腰上的高相等’的时候,发现利用“三角形的面积”很容易解决.你知道吗?”
小华思索了一会,对小明说:“这个方法真好,但我发现这种方法还可以用来证明‘等腰三角形底边上的任一点到两腰的距离之和等于一腰上的高’.”
小明苦苦思索,但仍没有解决,就请小华帮助他,你知道小华是如何帮助小明的吗?请写出你的思路过程.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
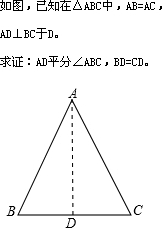 小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).
小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时,画出图形,写出“已知”、“求证”(如图).查看答案和解析>>
科目:初中数学 来源:河北省模拟题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年浙江省绍兴市绍兴县夏履镇中学中考数学模拟试卷(解析版) 题型:解答题
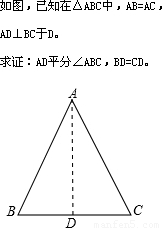
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com