Question

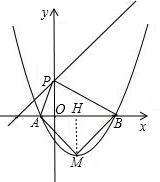
已知在同一直角坐标系中，直线l：y=x-3k+6与y轴交于点P，M是抛物线C：y=x²-2 （k+2）x+8k的顶点．
（1）求证：当k≠2时，抛物线C与x轴必定交于两点；
（2）A、B是抛物线c与x轴的两交点，A、B在y轴两侧，且A在B的左边，判断：直线l能经过点B吗？（需写出判断的过程）
（3）在（2）的条件下，是否存在实数k，使△ABP和△ABM的面积相等？如果存在，请求出此时抛物线C的解析式；若不存在，请说明理由．

Answer 1

分析：（1）列出抛物线的△，用配方法整理得出△＞0即可；
（2）解方程x²-2 （k+2）x+8k=0，得抛物线与x轴两交点的横坐标为4，2k，因为A、B在y轴两侧，且A在B的左边，可知
A（2k，0），B（4，0），将B代入y=x-3k+6中得k=

10

3

，这与A（2k，0）在y轴左边矛盾，故直线l不可能经过点B；
（3）将抛物线写成顶点式为y=[x-（k+2）]²-（k-2）²，作MH⊥x轴于H，则MH=（k-2）²，已知OP=-3k+6，当S_△ABP=S_△ABM时，MH=OP，列方程求k即可．

解答：（1）证明：在抛物线C中，
△=4（k+2）²-32k
=4k²-16k+16
=4（k-2）²．
∵当k≠2时，4（k-2）²＞0，
∴方程x²-2（k+2）x+8k=0有两个不相等的实数根．
∴当k≠2时，抛物线C与x轴必定交于两点；

（2）解：方程x²-2（k+2）x+8k=0，
得x₁=4，x₂=2k，
∵点A、B在y轴两侧，且A在B的左边，
∴k＜0，点B（4，0），
把点B（4，0）代入y=x-3k+6，
得k=

10

3

＞0，与“k＜0”不符，
∴直线l不可能经过点B．

（3）存在．
∵y=x²-2（k+2）x+8k
=[x-（k+2）]²-（k-2）²，
作MH⊥x轴于H，则MH=（k-2）²，
∵k＜0，∴-3k+6＞0，
∴OP=-3k+6，
由S_△ABP=S_△ABM，得-3k+6=（k-2）²，
解得k₁=-1，k₂=2（舍去），
∴存在实数k=-1，使得S_△ABP=S_△ABM，
此时，抛物线C的解析式是y=x²-2x-8．

点评：本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法．在求有关动点问题时要注意分析题意分情况讨论结果．