练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    . （本题8分）

    如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且

    ∠DBA=∠BCD．

    （1）根据你的判断：BD是⊙O的切线吗？为什么？．

    （2）若点E是劣弧BC上一点，AE与BC相交于点F，

    且△BEF的面积为10，cos∠BFA＝，那么，你能求

    出△ACF的面积吗？若能，请你求出其面积；若不能，请说明理由．

     

     

     

     

     

     

     

    【答案】

     

     

    解：（1）BD是⊙O的切线…………1’

              连接OB

    ∵AC是⊙O的直径

    ∴∠ABC=900

    ∴∠1+∠C=900

    ∵OA=OB

    ∴∠1=∠2

    ∴∠2+∠C=900

    ∵∠3=∠C

    ∴∠2+∠3=900

    ∴DB是⊙O的切线………………………4’

          （2）在Rt△ABF中，

    ∵cos∠BFA=   ∴ …………………5’

    ∵∠E=∠C，∠4=∠5

     ∴△EBF∽△CAF

    ∴…………………………7’

    即   解之得：S△ACF=22.5…………8’

     

     【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （本题6分）如图：直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B＝67°，∠ACB＝74°，

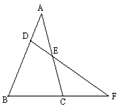
    ∠AED＝48°，求∠BDF的度数。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题8分）如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（＋1，＋4），从B到A记为：A→B（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中

    （1）A→C（     ，    ），B→C（    ，     ）,

    C→     （＋1，     ）； （3分）

    （2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；（3分）

    （3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋2），（＋2，－1），

    （－2，＋3），（－1，－2），请在图中标出P的位置。（2分）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题12分）如图，∠AOB为直角，∠BOC为锐角，且OM平分∠AOC，ON平分∠BOC．
    【小题1】⑴若∠BOC＝50°，试求∠MON的度数；
    【小题2】⑵如果⑴中的∠BOC＝α（α为锐角），其他条件不变，试求∠MON的度数；
    【小题3】⑶如果⑴中∠AOB＝β，其他条件不变，你能求出∠MON的度数吗？
    【小题4】⑷从⑴⑵⑶的结果，你能看出什么规律？

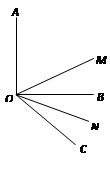
    查看答案和解析>>

    科目：初中数学 来源：2012届湖北省黄石四中七年级下学期期中考试数学卷 题型：解答题

    （本题6分）如图：直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B＝67°，∠ACB＝74°，

    ∠AED＝48°，求∠BDF的度数。

    查看答案和解析>>

    科目：初中数学 来源：2011届河南省三门峡中考一模数学试卷 题型：解答题

    （本题10分）如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到到B′的位置，AB′与CD交于点E.
    （1）求证：△AED≌△CEB′
    （2）若AB = 8，DE = 3，点P为线段AC上任意一点，PG⊥AE于G，PH⊥BC于H.求PG + PH的值.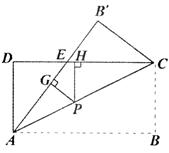

    查看答案和解析>>

    同步练习册答案