
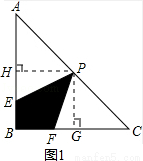
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;
(1)求证:∠APE=∠CFP;
(2)记△CPF的面积为S2,CF=x,y=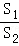 .
.
①求y关于x的函数解析式和自变量的取值范围,并求y的最大值.
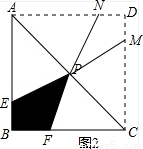
②在图中作四边形PEBF关于AC的对称图形,若它们关于点P中心对称,求y的值.
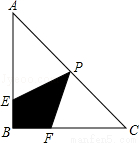
(1)见解析;
(2)①则y关于x的函数解析式为:y=﹣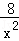 +
+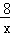 ﹣1,(2≤x≤4),y的最大值为1;
﹣1,(2≤x≤4),y的最大值为1;
②图见解析, y=2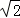 ﹣2.
﹣2.
【解析】
试题分析:(1)分别证出∠APE+∠FPC=∠CFP+∠FPC=135°,即可得出∠APE=∠CFP;
(2)①先证出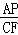 =
=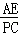 ,再根据AP=CP=2
,再根据AP=CP=2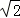 ,得出AE=
,得出AE=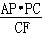 =
= ,过点P作PH⊥AB于点H,PG⊥BC于点G,求出S△APE=
,过点P作PH⊥AB于点H,PG⊥BC于点G,求出S△APE=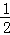 PH•AE=
PH•AE= ,S2=S△PCF=
,S2=S△PCF=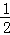 CF×PG=x,再根据S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣
CF×PG=x,再根据S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣ ﹣x,再代入y=
﹣x,再代入y=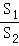 得出y=﹣8(
得出y=﹣8( ﹣
﹣ )2+1,最后根据2≤x≤4,得出
)2+1,最后根据2≤x≤4,得出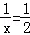 时,y取得最大值,最后将x=2代入y=
时,y取得最大值,最后将x=2代入y=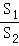 即可求出y最大=1.
即可求出y最大=1.
②根据图中两块阴影部分图形关于点P成中心对称,得出阴影部分图形自身关于直线BD对称,AE=FC,从而得出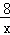 =x,求出x=2
=x,求出x=2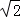 ,最后把
,最后把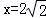 代入y=﹣
代入y=﹣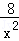 +
+ ﹣1即可.
﹣1即可.
试题解析:(1)∵∠EPF=45°,
∴∠APE+∠FPC=180°﹣45°=135°;
在等腰直角△ABC中,∠PCF=45°,
则∠CFP+∠FPC=180°﹣45°=135°,
∴∠APE=∠CFP.
(2)①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,
则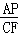 =
=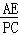 .
.
在等腰直角△ABC中,AC=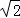 AB=4
AB=4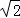 ,
,
又∵P为AC的中点,则AP=CP=2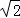 ,
,
∴AE=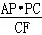 =
=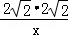 =
=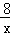 .
.
如图1,过点P作PH⊥AB于点H,PG⊥BC于点G,
P为AC中点,则PH∥BC,且PH= BC=2,同理PG=2.
BC=2,同理PG=2.
S△APE= PH•AE=
PH•AE= ×2×
×2×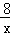 =
=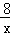 ,
,
S2=S△PCF= CF×PG=
CF×PG= ×x×2=x,
×x×2=x,
∴S1=S△ABC﹣S△APE﹣S△PCF= ×4×4﹣
×4×4﹣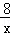 ﹣x=8﹣
﹣x=8﹣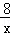 ﹣x,
﹣x,
∴y=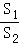 =
= =﹣
=﹣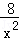 +
+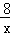 ﹣1=﹣8(
﹣1=﹣8( ﹣
﹣ )2+1,
)2+1,
∵E在AB上运动,F在BC上运动,且∠EPF=45°,
∴2≤x≤4.
即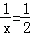 时,y取得最大值.
时,y取得最大值.
而x=2在x的取值范围内,将x=2代入y=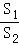 =﹣8(
=﹣8( ﹣
﹣ )2+1,得y最大=1.
)2+1,得y最大=1.
则y关于x的函数解析式为:y=﹣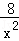 +
+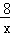 ﹣1,(2≤x≤4),y的最大值为1.
﹣1,(2≤x≤4),y的最大值为1.
②如图2所示:
图中两块阴影部分图形关于点P成中心对称,则阴影部分图形自身关于直线BD对称,
此时EB=BF,即AE=FC,
则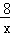 =x,
=x,
解得x1=2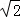 ,x2=﹣2
,x2=﹣2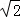 (舍去),
(舍去),
将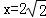 代入y=﹣
代入y=﹣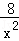 +
+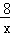 ﹣1,得y=2
﹣1,得y=2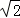 ﹣2.
﹣2.
考点:几何变换综合题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:选择题
一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )
A. 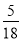 B.
B.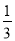 C.
C.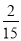 D.
D.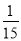
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市徐汇区中考二模数学试卷(解析版) 题型:选择题
“大衣哥”朱之文是从“我是大明星”这个舞台走出来的民间艺人.受此影响,卖豆腐的老张也来参加节目的海选,当天共有15位选手参加决逐争取8个晋级名额.已知他们的分数互不相同,老张要判断自己是否能够晋级,只要知道下列15名选手成绩统计量中的( )
A.众数 B.方差 C.中位数 D.平均数
查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽省安庆市中考二模数学试卷(解析版) 题型:解答题
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
(1)先将△ABC向右平移3个单位后得到△A1B1C1,再将△A1B1C1绕点B1按逆时针方向旋转90°后得到△A2B1C2;试在正方形网格中画出上述二次变换所得到的图形;
(2)求线段A1C1旋转得到A2C2的过程中,线段A1C1所扫过的面积.

查看答案和解析>>
科目:初中数学 来源:2016届初中数学湘教版七年级上第4章练习卷(解析版) 题型:解答题
有一火车要以每分钟600米的速度过完第一、第二两座铁桥,过第二座铁桥比过第一座铁桥多5秒时间,又知第二座铁桥的长度比第一座铁桥长度的2倍短50米,试求两座铁桥的长分别为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com