解:(1)根据①当三边长分别为3、4、5时,3
2+4
2=5
2;
②当三边长分别为6、8、10时,6
2+8
2=10
2;
③当三边长分别为5、12、13时,5
2+12
2=13
2; …得到一个规律,直角三角形斜边的平方等于两直角边的平方和,
则在直角△ABC中,若∠B=90°,则它的三边长满足:AB
2+BC
2=AC
2;
(2)设BF=x,则CF=5-x,S
△DCF=

DC•CF=

=20-4x,S
△BEF=
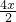
=2x,S
△DAE=

=10
而S
△DEF=16,且矩形ABCD的面积为5×8=40,
所以(20-4x)+2x+10+16=40,解得x=3,
则根据勾股定理得:EF=

=5,设D到直线EF的距离为d,
所以

×5d=16,
解得d=

.
故答案为:AB
2+BC
2=AC
2.
分析:(1)根据题中已知式子,归纳总结出直角三角形三边的平方关系为两直角边的平方和等于斜边的平方,即可得出直角△ABC的三边长满足的关系式;
(2)要求D到直线EF的距离,即为三角形DEF的边EF上的高,根据三角形EDF的面积为16,所以只需求出EF的长度,利用三角形的面积公式即可求出,由E为AB的中点,设BF为x,则CF=5-x,然后利用x,根据三角形的面积公式分别表示出△DCF,△AED,及三角形EFB的面积,根据三角形DEF的面积为16和矩形的面积为40,由矩形的面积等于图中四个三角形的面积之和列出关于x的方程,求出方程的解即可得到x的值,然后利用勾股定理求出EF,利用三角形的面积公式即可求出D到直线EF的距离.
点评:此题考查学生灵活运用三角形的面积公式化简求值,掌握矩形的性质及勾股定理的运用,理解点到直线的距离的定义,是一道综合题.

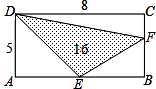 小明在研究直角三角形的边长时,发现了下面的式子:
小明在研究直角三角形的边长时,发现了下面的式子: DC•CF=
DC•CF= =20-4x,S△BEF=
=20-4x,S△BEF=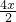 =2x,S△DAE=
=2x,S△DAE= =10
=10 =5,设D到直线EF的距离为d,
=5,设D到直线EF的距离为d, ×5d=16,
×5d=16, .
.

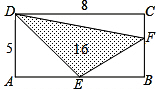 小明在研究直角三角形的边长时,发现了下面的式子:
小明在研究直角三角形的边长时,发现了下面的式子:
