
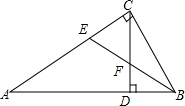
 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )| A. | ①③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
分析 ①利用外角的性质可得∠1=∠A+∠6,∠2=∠4+∠5,由角平分线的性质可得:∠5=∠6,由同角的余角相等可得:∠A=∠4,进而可得∠1=∠2,即∠CFE=∠CEF;
②采用分析法,若∠FCB=∠FBC,即∠4=∠5,由(1)可知:∠A=∠4,进而∠A=∠5=∠6,然后由直角三角形两锐角互余可得∠A=30°,即只有当∠A=30°时,∠FCB=∠FBC而已知没有这个条件;
③由同角的余角相等可得:∠A=∠4,即∠A=∠DCB;
④由∠1=∠2,∠1与∠5互余,可得∠2与∠5互余,即:∠CFE与∠CBF互余.
解答 解:如图所示,
①∵BE平分∠ABC,
∴∠5=∠6,
∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
∵∠1=∠A+∠6,∠2=∠4+∠5,
∠1=∠2,
故∠CFE=∠CEF,所以①正确;
②若∠FCB=∠FBC,即∠4=∠5,
由(1)可知:∠A=∠4,
∴∠A=∠5=∠6,
∵∠A+∠5+∠6=180°,
∴∠A=30°,
即只有当∠A=30°时,∠FCB=∠FBC而已知没有这个条件,故②错误;
③∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
即∠A=∠DCB,故③正确;
④∵∠1=∠2,∠1+∠5=90°,
∴∠2+∠5=90°,
即:∠CFE与∠CBF互余,故④正确.
故选A.
点评 本题考查了等腰三角形的判定,角平分线的定义,直角三角形两锐角互余的性质,同角的余角相等的性质,利用阿拉伯数字加弧线表示角更形象.


科目:初中数学 来源: 题型:解答题
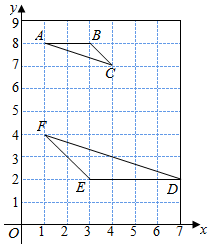 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com