练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

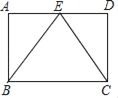
    【题目】如图，在矩形ABCD中，点E是边AD的中点，连接BE、CE．

    (1)求证：△ABE≌△DCE；

    (2)当BC＝2AB，求∠BEC的大小．

    【答案】(1)见解析；(2)∠BEC＝90°.

    【解析】

    （1）根据SAS即可证明；
    （2）只要证明△ABE，△DEC都是等腰直角三角形即可解决问题；

    (1)证明：∵四边形ABCD是矩形，

    ∴AB＝DC，∠A＝∠D＝90°.

    ∵点E是边AD的中点，

    ∴AE＝DE，∴△ABE≌DCE(SAS)．

    (2)∵四边形ABCD是矩形，

    ∴AD＝BC，∠A＝90°.

    ∵BC＝2AB，∴AD＝2AB．

    ∵AD＝2AE，∴AE＝AB，

    ∴∠AEB＝∠ABE＝45°.

    同理可得∠DEC＝45°，

    ∴∠BEC＝180°－∠AEB－∠DEC＝180°－45°－45°＝90°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处．若AE=BE，则长AD与宽AB的比值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度，随机抽取了部分学生进行调查（每人限选1项），现将调查结果绘制成如下两幅不完整的统计图，根据图中所给的信息解答下列问题．

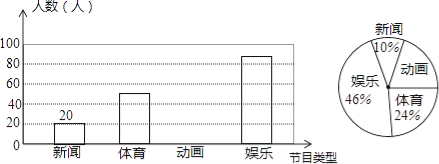
    （1）喜爱动画的学生人数和所占比例分别是多少？

    （2）请将条形统计图补充完整；

    （3）若该校共有学生1000人，依据以上图表估计该校喜欢体育的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，方格图中每个小正方形的边长为1，点A、B、C都是格点．

    （1）画出△ABC关于直线MN对称的△A1B1C1；

    （2）直接写出AA1的长度；

    （3）如图2，A、C是直线MN同侧固定的点，D是直线MN上的一个动点，在直线MN上画出点D，使AD+DC最小．（保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标平面内有两点A（0，2）、B（﹣2，0）、C（2，0）．

    （1）△ABC的形状是 等腰直角三角形；

    （2）求△ABC的面积及AB的长；

    （3）在y轴上找一点P，如果△PAB是等腰三角形，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李晖到“宇泉牌”服装专卖店做社会调查．了解到商店为了激励营业员的工作积极性，实行“月总收入＝基本工资＋计件奖金”的方法，并获得如下信息：

    营业员

    小俐

    小花

    月销售件数（件）

    200

    150

    月总收入（元）

    1400

    1250

    假设月销售件数为件，月总收入为元，销售每件奖励元，营业员月基本工资为元．

    （1）求的值；

    （2）若营业员小俐某月总收入不低于元，那么小俐当月至少要卖服装多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器，若购电脑机箱10台和液液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液示器5台，共需要资金4120元．

    （1）每台电脑机箱、液晶显示器的进价各是多少元？

    （2）该经销商购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案？哪种方案获利最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

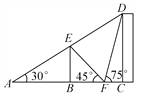
    【题目】如图，楼房CD旁边有一池塘，池塘中有一电线杆BE高10米，在池塘边F处测得电线杆顶端E的仰角为45°，楼房顶点D的仰角为75°，又在池塘对面的A处，观测到A，E，D在同一直线上时，测得电线杆顶端E的仰角为30°.

    (1)求池塘A，F两点之间的距离；

    (2)求楼房CD的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，如图（2），设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．

    （1）求证：BD1=CE1；（2）当∠CPD1=2∠CAD1时，求CE1的长；

    （3）连接PA，△PAB面积的最大值为　　．（直接填写结果）

    查看答案和解析>>

    同步练习册答案