
分析 (1)设购进甲型电视机x台,乙型电视机y台,丙型电视机z台,分①只购进甲、乙两种不同型号的电视机、②只购进甲、丙两种不同型号的电视机、③只购进乙、丙两种不同型号的电视机三种情况考虑,根据三种型号电视机的出厂价、购进台数以及购机的总花费为90000元即可得出二元一次方程组,解方程组后再根据x、y、z均为正整数即可得出结论;
(2)根据总利润=每台利润×购进台数即可求出各购机方案的利润,比较后即可得出结论.
解答 解:(1)设购进甲型电视机x台,乙型电视机y台,丙型电视机z台,
①当购进甲、乙两种不同型号的电视机时,
$\left\{\begin{array}{l}{x+y=50}\\{1500x+2100y=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=25}\\{y=25}\end{array}\right.$;
②当购进甲、丙两种不同型号的电视机时,
$\left\{\begin{array}{l}{x+z=50}\\{1500x+2500z=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35}\\{z=15}\end{array}\right.$;
③当购进乙、丙两种不同型号的电视机时,
$\left\{\begin{array}{l}{y+z=50}\\{2100y+2500z=90000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{y=87.5}\\{z=-37.5}\end{array}\right.$(舍去).
综上所述:可有两种进货方案,方案一:购进甲型电视机25台、乙型电视机25台;方案二:购进甲型电视机35台、丙型电视机15台.
(2)当选择方案一时:利润=150×25+200×25=8750(元);
当选择方案二时:利润=150×35+250×15=9000(元).
∵8750<9000,
∴购进甲型电视机35台、丙型电视机15台可使销售时获利最多.
点评 本题考查了二元一次方程组的应用,根据数量关系列出二元一次方程组是解题的关键.


科目:初中数学 来源: 题型:解答题
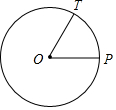 如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于点S.
如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于点S.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
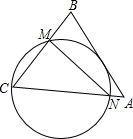 如图,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是3.
如图,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
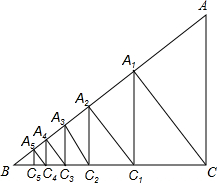 如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)
如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
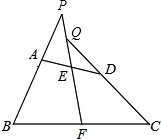 如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
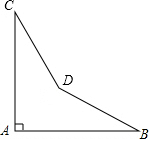 某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
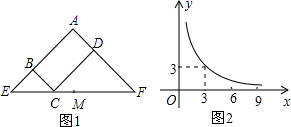 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )| A. | 当x=3时,EC<EM | B. | 当x=9时,EC<EM | ||
| C. | 当x增大时,BE•DF的值不变 | D. | 当x增大时,EC•CF的值增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com