
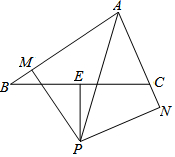
 如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.
如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN. 分析 因为ED是BC的垂直平分线,那么BD=CD,而AD是∠BAC的平分线,DM⊥AB,DN⊥AC,根据角平分线的性质可得DM=DN,再根据HL可判定Rt△BMD≌Rt△CND,从而有BM=CN.
解答 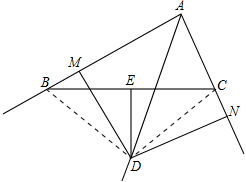 证明:连接BD,CD,如图,
证明:连接BD,CD,如图,
∴DE是BC的垂直平分线,
∴BD=CD,
∵AD是∠BAC的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△BMD和Rt△CND中,
$\left\{\begin{array}{l}{BD=CD}\\{DM=DN}\end{array}\right.$,
∴Rt△BMD≌Rt△CND(HL),
∴BM=CN
点评 本题考查了全等三角形的判定和性质、线段垂直平分线的性质,解题的关键是掌握垂直平分线的定义以及性质,掌握角平分线的性质以及具体的应用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
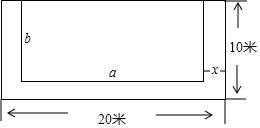 如图,有一块长为20米,宽10米的长方形土地,现将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:
如图,有一块长为20米,宽10米的长方形土地,现将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )
如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2-2x+3.
已知二次函数y=-x2-2x+3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com