
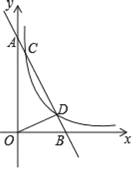
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=![]() (m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.动点P,Q从点A同时出发,点P沿AB向终点B运动;点Q沿AC→CB向终点B运动,速度都是1cm/s.当一个点到达终点时,另一个点同时停止运动.设点P运动的时间为t(s),在运动过程中,点P,点Q经过的路线与线段PQ围成的图形面积为S(cm2).
(1)AC=_________cm;
(2)当点P到达终点时,BQ=_______cm;
(3)①当t=5时,s=_________;
②当t=9时,s=_________;
(4)求S与t之间的函数解析式.
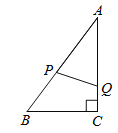

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
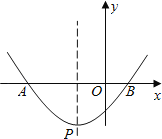
【题目】如图,抛物线y=![]() x2+x﹣
x2+x﹣![]() 与x轴相交于A,B两点,顶点为P.
与x轴相交于A,B两点,顶点为P.
(1)求点A,点B的坐标;
(2)在抛物线上是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:

请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
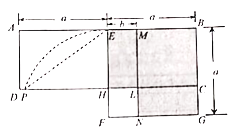
【题目】如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了![]() .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则
.现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上![]() 、
、![]() 、
、![]() (每个字母分别代表一位同学,其中
(每个字母分别代表一位同学,其中![]() 、
、![]() 分别代表两位女生,
分别代表两位女生,![]() 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。
代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。
(1)求李老师第一次摸出的乒乓球代表男生的概率;
(2)请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组数据的中位数是________,乙组数据的众数是________;
(2)已知甲组数据的方差是1.4分2 ,则成绩较为整齐的是哪个队?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com