
【题目】一副直角三角板由一块含30°的直角三角板与一块等腰直角三角板组成,且含30°角的三角板的较长直角边与另一三角板的斜边相等(如图1)

(1)如图1,这副三角板中,已知AB=2,AC= ,A′D=
(2)这副三角板如图1放置,将△A′DC′固定不动,将△ABC通过旋转或者平移变换可使△ABC的斜边BC经过△A′DC′′的直角顶点D.
方法一:如图2,将△ABC绕点C按顺时针方向旋转角度α(0°<α<180°)
方法二:如图3,将△ABC沿射线A′C′方向平移m个单位长度
方法三:如图4,将△ABC绕点A按逆时针方向旋转角度β(0°<β<180°)
请你解决下列问题:
①根据方法一,直接写出α的值为: ;
②根据方法二,计算m的值;
③根据方法三,求β的值.
(3)若将△ABC从图1位置开始沿射线A′C′平移,设AA′=x,两三角形重叠部分的面积为y,请直接写出y与x之间的函数关系式和相应的自变量x的取值范围.
【答案】(1)![]() ;(2)①15°;②
;(2)①15°;②![]() ;③30°;(3)
;③30°;(3)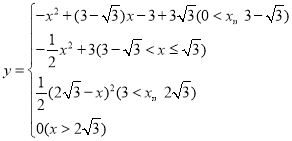
【解析】
(1)根据直角三角形中30°的直角边所对的直角边等于斜边的一半,即可求得BC的长,然后根据勾股定理即可求得AC的长;
(2)①根据三角板的度数即可求解;
②作DH⊥A′C于H,易证△CDH∽△CBA,根据相似三角形的对应边的比相等,即可求得CH的长,进而求得CC′;
③作DH⊥A′C′于H,AG⊥BC于G,可以证得Rt△AGD≌Rt△DHA,则BC∥AC′,利用平行线的性质即可求解;
(3)分0<x≤![]() ,
,![]() <x≤
<x≤![]() ,
,![]() <x≤2
<x≤2![]() ,x>2
,x>2![]() 四种情况即可求解.
四种情况即可求解.
(1)∵直角△ABC中,∠BAC=30°,
∴BC=2AB=4,
∴AC=![]() =2
=2![]() ,
,
在等腰直角直角△A′DC′中,A′C′=2![]() ,
,
∴A′D=![]() A′C′=
A′C′=![]() ;
;
(2)①α=45°﹣30°=15°;
②作DH⊥A′C于H,则DH=![]() A′C′=C′H=
A′C′=C′H=![]() ,
,
∵DH∥AB,
∴△CDH∽△CBA.
∴![]() ,即
,即![]() ,
,
∴CH=3.
∴CC′=CH﹣C′H=3﹣![]() ,即m=CC′=3﹣
,即m=CC′=3﹣![]() ;
;
③作DH⊥A′C′于H,AG⊥BC于G,
由已知:DH=![]()
![]() ,
,
AG×BC=AB×AC,
∴AG=![]() =
=![]() ,
,
∴AG=DH.
在Rt△AGD和Rt△DHA中:![]() ,
,
∴Rt△AGD≌Rt△DHA,
∴∠GDA=∠DAH=45°,
∴BC∥AC′,
∴β=∠BCA=30°;
(3)y=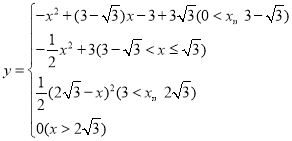 .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
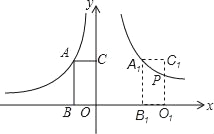
【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣![]() (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=
(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=![]() (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
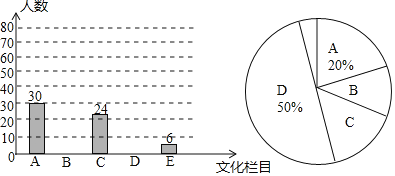
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中,OA在x轴上,已知∠COD=∠OAB=90°,OC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值.
(2)把△OCD沿射线OB移动,当点D落在y=![]() 图象上时,求点D经过的路径长.
图象上时,求点D经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.
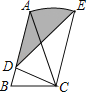
查看答案和解析>>
科目:初中数学 来源: 题型:
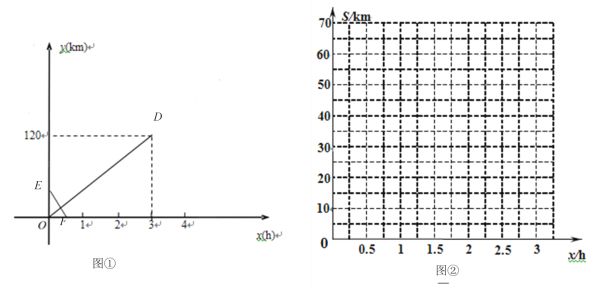
【题目】已知A,C,B三地依次在一条直线上,甲骑摩托车直接从C地前往B地;乙开车以80km/h的速度从A地前往B地,在C地办理事务耽误1 h后,继续前往B地.已知两人同时出发且速度不变,又恰好同时到达B地.设出发x h后甲乙两人离C地的距离分别为y1 kmy2 km,图①中线段OD表示y1与x的函数图像,线段EF表示y2与x函数的部分图像.
(1)甲的速度为 km/h,点E坐标为 ;
(2)求线段EF所表示的y2与x之间的函数表达式;
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx经过点A(4,0),点B是其顶点,∠AOB=45°,OC⊥OB交此抛物线于点C,动直线y=kx与抛物线交于点D,分别过点B、C作BE、CF垂直动直线y=kx于点E、F.
(1)求此抛物线的解析式;
(2)当直线y=kx把∠AOC分成的两个角的度数之比恰好为1:2时,求k的值;
(3)BE+CF是否存在最大值?若存在,请直接写出此最大值和此时k的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com