
【题目】如图,矩形![]() 和
和![]() ,
,![]() .
.
![]() 画出矩形
画出矩形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后的矩形
后的矩形![]() ,并写出
,并写出![]() 的坐标为________,点
的坐标为________,点![]() 运动到点
运动到点![]() 所经过的路径的长为________;
所经过的路径的长为________;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为________,请画一条直线
的坐标为________,请画一条直线![]() 平分矩形
平分矩形![]() 与
与![]() 组成图形的面积(保留必要的画图痕迹).
组成图形的面积(保留必要的画图痕迹).

 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC中点连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④![]() ,其中结论正确的个数有( )
,其中结论正确的个数有( )
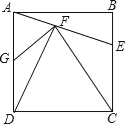
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E在BC边上,点F在AC边上,将△ABD沿着AD翻折,使点B和点E重合,将△CEF沿着EF翻折,点C恰与点A重合.结论:①∠BAC=90°,②DE=EF,③∠B=2∠C,④AB=EC,正确的有( )
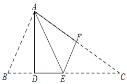
A.①②③④B.③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣活动课上,小明将等腰△ABC的底边BC与直线1重合,问:
(1)已知AB=AC=6,∠BAC=120°,点P在BC边所在的直线l上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小明发现AP的最小值是 ;
(2)为进一步运用该结论,小明发现当AP最短时,在Rt△ABP中,∠P=90°,作了AD平分∠BAP,交BP于点D,点E、F分别是AD、AP边上的动点,连接PE、EF,小明尝试探索PE+EF的最小值,为转化EF,小明在AB上截取AN,使得AN=AF,连接NE,易证△AEF≌△AEN,从而将PE+EF转化为PE+EN,转化到(1)的情况,若BP=3![]() ,AB=6,AP=3,则PE+EF的最小值为 ;
,AB=6,AP=3,则PE+EF的最小值为 ;
(3)请应用以上转化思想解决问题(3),在直角△ABC中,∠C=90°,∠B=30°,AC=10,点D是CD边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,求线段CP的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在x轴上,BC⊥y轴于C,点B的横坐标为a,AB=2a,∠B=120°,在y轴上找一点P,使PA+PB最小,请画出点P,并求PA+PB的最小值.
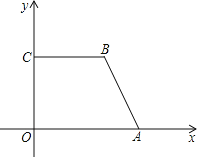
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=-2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
(1)求证:△ADM∽△AOB.
(2)如果⊙M的半径为2![]() ,请写出点M的坐标,并写出以点
,请写出点M的坐标,并写出以点![]() 为顶点,且过点M的抛物线的函数表达式.
为顶点,且过点M的抛物线的函数表达式.
(3)在(2)的条件下,试问在此抛物线上是否存在点P,使以P,A,M三点为顶点的三角形与△AOB相似?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com