
【题目】温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地![]() 台,杭州厂可支援外地
台,杭州厂可支援外地![]() 台.现在决定给武汉
台.现在决定给武汉![]() 台,南昌
台,南昌![]() 台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为
台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为![]() 台.
台.
南昌 | 武汉 | |
温州厂 |
|
|
杭州厂 |
|
|
(![]() )用
)用![]() 的代数式来表示总运费(单位:百元).
的代数式来表示总运费(单位:百元).
(![]() )若总运费为
)若总运费为![]() 元,则杭州运往南昌的机器应为多少台?
元,则杭州运往南昌的机器应为多少台?
(![]() )试问有无可能使总运费是
)试问有无可能使总运费是![]() 元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
【答案】(![]() )总运费为
)总运费为![]() 百元;(
百元;(![]() )总运费为
)总运费为![]() 元,杭州运往南昌的机器应为
元,杭州运往南昌的机器应为![]() 台;(
台;(![]() )总运费不可能是
)总运费不可能是![]() 元.
元.
【解析】试题分析:(1)设总费用为W百元,由杭州运往南昌x台,运往武汉(4-x)台,
温州运往南昌(6-x)台,运往武汉(4+x)台,根据总费用=各部分运费之和就可以求出结论;
(2)当W=8200代入(1)的解析式就可以求出结论;
(3)当W=7400代入解析式求出x的值就可以判定结论.
试题解析:解:(1)设总费用为W百元,由杭州运往南昌x台,运往武汉(4-x)台,
温州运往南昌(6-x)台,运往武汉(4+x)台,根据题意得:
W=4(6-x)+8(4+x)+3x+5(4-x)=2x+76,
∴总运费为(2x+76)百元.
(2)当W=8200元=82百元时,76+2x=82,解得x=3.
答:总运费为8200元,杭州运往南昌的机器应为3台.
(3)当W=7400元=74百元时,
74=2x+76,解得:x=-1,
∵0≤x≤4,
∴x=-1不符合题意,
总运费不可能是7400元.


科目:初中数学 来源: 题型:
【题目】在数轴上,一只蚂蚁从原点出发,先向右爬行了4个单位长度到达点A,再向右爬行了2个单位长度到达点B,然后又向左爬行了10个单位长度到达点C.
(1)画出数轴,并在数轴上表示出A、B、C三点;
(2)根据点C在数轴上的位置,点C可以看作是蚂蚁从原点出发,向哪个方向爬行了几个单位长度得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
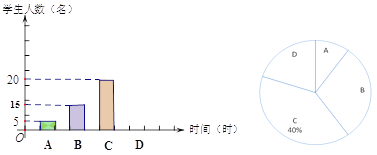
【题目】某校在九年级学生中开展以“每天数学家庭作业完成时间”设置的一个问题,有以下选项:
A.0~0.5小时B.0.5~1个小时 C.1个小时~1.5个小时 D.1.5个小时以上
在随机调查了九(1)班学生后,根据相关数据给出如图所示的统计图.
(1)该校九(1)班学生 人;做数学家庭作业1.5个小时以上的占 ;
(2)补全频数直方图;
(3)已知该校九年级共400名学生,据此推算,该校九年级学生中,“做数学家庭作业1.5个小时以上”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
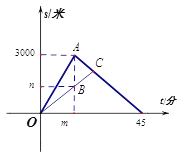
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸距出发地1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
(1)图中![]() ,
, ![]() ;
;
(2)求小明和爸爸相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE. 
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由. 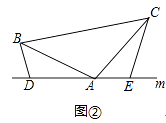
查看答案和解析>>
科目:初中数学 来源: 题型:
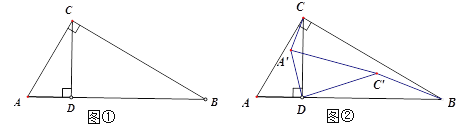
【题目】如图①,在Rt△ABC中,∠C=90°, ∠B=30°,AC=1,CD⊥AB,垂足为D,现将△ACD绕D点顺时针旋转![]() 得到△A‘C’D, 旋转时间为t秒,△ACD绕D点旋转的角速度
得到△A‘C’D, 旋转时间为t秒,△ACD绕D点旋转的角速度![]() /秒(每秒转10度) .
/秒(每秒转10度) .
(1)旋转时间t= 秒时,A‘C’∥AB;
(2)△ACD绕D点顺时针旋转一周(3600),斜边AC扫过的面积为 ;
(3)如图②,连接A’C、 C’B.
①若6<t<9,求证: ![]() 为定值;
为定值;
②当t>9时,上述结论还成立吗?如成立直接写出比值,不成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
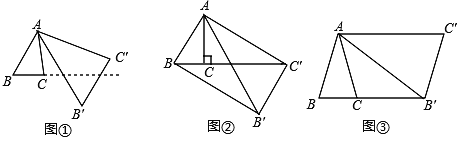
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com