
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数学问题中,我们常用几何方法解决代数问题,借助数形结合的方法使复杂问题简单化.
材料一:我们知道|a|的几何意义是:数轴上表示数a的点到原点的距离;|a﹣b|的几何意义是:数轴上表示数a,b的两点之间的距离;|a+b|的几何意义是:数轴上表示数a,﹣b的两点之间的距离;根据绝对值的几何意义,我们可以求出以下方程的解.
(1)|x﹣3|=4
解:由绝对值的几何意义知:
在数轴上x表示的点到3的距离等于4
∴x1=3+4=7,x2=3﹣4=﹣1
(2)|x+2|=5
解:∵|x+2|=|x﹣(﹣2)|,∴其绝对值的几何意义为:在数轴上x表示的点到﹣2的距离等于5.∴x1=﹣2+5=3,x2=﹣2﹣5=﹣7
材料二:如何求|x﹣1|+|x+2|的最小值.
由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和,要使和最小,则表示数x的这点必在﹣2和1之间(包括这两个端点)取值.
∴|x﹣1|+|x+2|的最小值是3;由此可求解方程|x﹣1|+|x+2|=4,把数轴上表示x的点记为点P,由绝对值的几何意义知:当﹣2≤x≤1时,|x﹣1|+|x+2|恒有最小值3,所以要使|x﹣1|+|x+2|=4成立,则点P必在﹣2的左边或1的右边,且到表示数﹣2或1的点的距离均为0.5个单位.
故方程|x﹣1|+|x+2|=4的解为:x1=﹣2﹣0.5=﹣2.5,x2=1+0.5=1.5.
阅读以上材料,解决以下问题:
(1)填空:|x﹣3|+|x+2|的最小值为 ;
(2)已知有理数x满足:|x+3|+|x﹣10|=15,有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小,求x﹣y的值.
(3)试找到符合条件的x,使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小,并求出此时的最小值及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
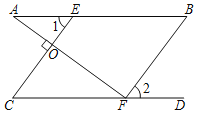
【题目】已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,
∠A+∠2=90°.求证:AB∥CD.
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
______________
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )
A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
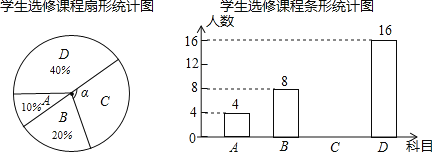
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点所对应的数分别为a、b.P为数轴上的一个动点.其中a,b满足(a﹣1)2+|b+5|=0,
(1)若点P为AB的中点,求P点对应的数.
(2)若点P从A点出发,以每秒2个单位的速度向左运动,t秒后,求P点所对应的数以及PB的距离.
(3)若数轴上点M、N所对应的数为m、n,其中A为PM的中点,B为PN的中点,无论点P在何处,![]() 是否为一个定值?若是,求出定值:若不是,请说明理由.
是否为一个定值?若是,求出定值:若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB= 90°,AC= 6cm, AB= 12cm,点P 从A出发沿AC向C点以1cm/s的速度匀速移动;点Q从C出发沿CB向B点以![]() cm/s的速度匀速移动,点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒;点0为AB的中点。
cm/s的速度匀速移动,点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒;点0为AB的中点。
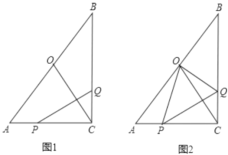
(1)当t=2时,求线段PQ的长度;
(2) 连接OC,当PQ⊥0C时,求出t的值;
(3)连结PO,PQ,是否存在t的值,使△OPQ成为以PQ为斜边的直角三角形?若存在,求出t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一个动点,由
上的一个动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),速度为每秒
不重合),速度为每秒![]() ,
,![]() 是
是![]() 延长线上一点,与点
延长线上一点,与点![]() 以相同的速度由
以相同的速度由![]() 向
向![]() 延长线方向运动(不与
延长线方向运动(不与![]() 重合),连结
重合),连结![]() 交AB于
交AB于![]() .
.


(1)如图1,若![]() ,
,![]() ,求点P运动几秒后,
,求点P运动几秒后,![]() .
.
(2)在(1)的条件下,作![]() 于F,在运动过程中,线段
于F,在运动过程中,线段![]() 长度是否发生变化,如果不变,求出
长度是否发生变化,如果不变,求出![]() 的长;如果变化,请说明理由.
的长;如果变化,请说明理由.
(3)如图3,当![]() 时,平行四边形的面积是
时,平行四边形的面积是![]() ,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称,若存在,求出a的值;若不存在,说明理由.
,那么在运动中是否存在某一时刻,点P,Q关于点E成中心对称,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
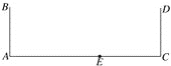
(1)在图中画出杨老师的位置(用线段FG表示),并画出光线,标明(太阳光、灯光);
(2)若上午上学时候高1米的木棒的影子为2米,杨老师身高为1.5米,他离里程碑E恰5米,求路灯高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com