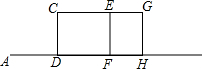Question

18．如图，A、B在一直线上，小明从点A出发沿AB方向匀速前进，4秒后走到点D，此时他（CD）在某一灯光下的影长为AD，继续沿AB方向以同样的速度匀速前进4秒后到点F，此时他（EF）的影长为2米，然后他再沿AB方向以同样的速度匀速前进2秒后达点H，此时他（GH）处于灯光正下方．
（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；
（2）求小明沿AB方向匀速前进的速度．

Answer 1

分析 （1）利用影长为AD，进而得出延长AC，HG得到O点，进而求出答案；
（2）利用相似三角形的性质得出$\frac{OG}{OH}$=$\frac{6x}{10x}$=$\frac{3}{5}$，$\frac{EG}{MH}$=$\frac{OG}{OH}$，进而得出x的值．

解答 解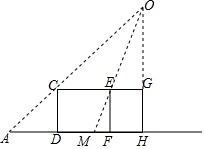：（1）如图所示：FM即为所求；

（2）设速度为x米/秒，
根据题意得CG∥AH，
∴△COG∽△OAH，
∴$\frac{CG}{AH}$=$\frac{OG}{OH}$，即：$\frac{OG}{OH}$=$\frac{6x}{10x}$=$\frac{3}{5}$，
又∵CG∥AH，
∴△EOG∽△OMH，
∴$\frac{EG}{MH}$=$\frac{OG}{OH}$，
即：$\frac{2x}{2+2x}$=$\frac{3}{5}$，
∴解得：x=$\frac{3}{2}$
答：小明沿AB方向匀速前进的速度为$\frac{3}{2}$米/秒．

点评 本题考查了相似三角形的应用以及中心投影，注意从实际问题中抽象出几何图形，然后利用相似比计算相应线段的长是解题关键．