
分析 先计算出AC=4,再利用面积法得到AB边长的高为$\frac{12}{5}$,由于把Rt△ABC绕AB旋转一周得到两个圆锥体,底面圆的半径为$\frac{12}{5}$,则利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算两圆锥的侧面积即可.
解答 解:AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
把Rt△ABC绕AB旋转一周得到两个圆锥体,底面圆的半径为$\frac{12}{5}$,
所以所得几何体的表面积=$\frac{1}{2}$•2π•$\frac{12}{5}$(3+4)=$\frac{84}{5}$π(cm2).
故答案为$\frac{84}{5}$π(cm2).
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.


科目:初中数学 来源: 题型:解答题
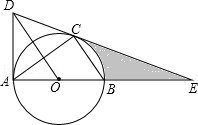 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是(1,1),△ABC的面积为4.
在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是(1,1),△ABC的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,E是AD上一点,且AD=3AE,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BE}$=-$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示)
如图,在?ABCD中,E是AD上一点,且AD=3AE,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{BE}$=-$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.(结果用$\overrightarrow{a}$、$\overrightarrow{b}$表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com