
【题目】如图,在等边三角形![]() 中,在
中,在![]() 边上取两点
边上取两点![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 则以
, 则以![]() ,
,![]() ,
,![]() 为边长的三角形的形状为( )
为边长的三角形的形状为( )

A.锐角三角形B.直角三角形C.钝角三角形D.随![]() ,
,![]() ,
,![]() 的值而定
的值而定
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 、
、![]() 是对角线
是对角线![]() 上的两点且
上的两点且![]() ,下列说法中正确的是( )
,下列说法中正确的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 为平行四边形;⑤
为平行四边形;⑤![]() ;⑥
;⑥![]() .
.

A.①⑥B.①②④⑥C.①②③④D.①②④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式及顶点坐标;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在抛物线的对称轴上是否存在一点P.使得以O、B、C、P四点为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为![]() ,较小的直角边长都为
,较小的直角边长都为![]() ,斜边长都为
,斜边长都为![]() ),大正方形的面积可以表示为
),大正方形的面积可以表示为![]() ,也可以表示为
,也可以表示为![]() ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为
,由此推导出重要的勾股定理:如果直角三角形两条直角边长为![]() ,斜边长为
,斜边长为![]() ,则
,则![]() .
.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在![]() 中,
中,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() ,
,![]() ,设
,设![]() ,求
,求![]() 的值.
的值.
(3)试构造一个图形,使它的面积能够解释![]() ,画在如图4的网格中,并标出字母
,画在如图4的网格中,并标出字母![]() 所表示的线段.
所表示的线段.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
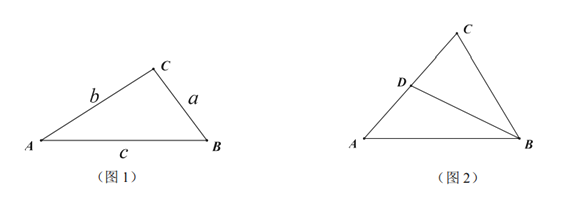
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 落在平行四边形
落在平行四边形![]() 所在平面内,
所在平面内,![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]()
![]() 判断
判断![]() 和
和![]() 的位置关系,并证明.
的位置关系,并证明.
![]() 在图1中,若
在图1中,若![]() ,是否存在
,是否存在![]() 恰好为直角三角形的情形?若存在,求出
恰好为直角三角形的情形?若存在,求出![]() 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由.
![]() 若将图中平行四边形纸片
若将图中平行四边形纸片![]() 换成矩形纸片
换成矩形纸片![]() ,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片
,沿对角线折叠发现所得图形是轴对称图形;将所得图形沿其对称轴再次折叠后,得到的仍是轴对称图形.则矩形纸片![]() 的长宽之比是多少?请直接写出结果.
的长宽之比是多少?请直接写出结果.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com