
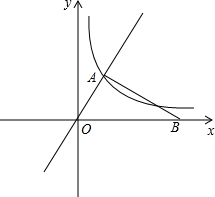
 如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.分析 (1)利用待定系数法先求出点A纵坐标,再求出反比例系数k即可.
(2)过点A作AC⊥OB⊥,垂足为点C,在RT△AOC中先求出OA,再在RT△AOB中求出OB即可解决问题.
(3)画出∠AOB的平分线OM,线段AB的垂直平分线EF,OM与EF的交点就是所求的点P,设点P(m,$\frac{\sqrt{3}}{3}$m),根据PA2=PB2,列出方程即可解决问题.
解答 解:(1)由题意,设点A的坐标为(1,m),
∵点A在正比例函数y=$\sqrt{3}$x的图象上,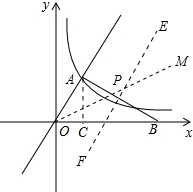
∴m=$\sqrt{3}$.∴点A的坐标(1,$\sqrt{3}$),
∵点A在反比例函数y=$\frac{k}{x}$的图象上,
∴$\sqrt{3}$=$\frac{k}{1}$,解得k=$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{\sqrt{3}}{x}$.
(2)过点A作AC⊥OB⊥,垂足为点C,
可得OC=1,AC=$\sqrt{3}$.
∵AC⊥OB,
∴∠ACO=90°.
由勾股定理,得AO=2,
∴OC=$\frac{1}{2}$AO,
∴∠OAC=30°,
∴∠ACO=60°,
∵AB⊥OA,
∴∠OAB=90°,
∴∠ABO=30°,
∴OB=2OA,
∴OB=4,
∴点B的坐标是(4,0).
(3)如图作∠AOB的平分线OM,AB的垂直平分线EF,OM与EF的交点就是所求的点P,
∵∠POB=30°,
∴可以设点P坐标(m,$\frac{\sqrt{3}}{3}$m),
∵PA2=PB2,
∴(m-1)2+($\frac{\sqrt{3}}{3}$m-$\sqrt{3}$)2=(m-4)2+($\frac{\sqrt{3}}{3}$m)2,
解得m=3,
∴点P的坐标是(3,$\sqrt{3}$).
点评 本题考查反比例函数与一次函数图象的交点问题,直角三角形中30度角所对的直角边等于斜边的一半,勾股定理等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会利用两点间距离公式列方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
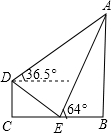 如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶上D点处测得条幅顶端A的仰角为36.5°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为64°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度为7.8米.
如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶上D点处测得条幅顶端A的仰角为36.5°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为64°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度为7.8米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
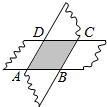 如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.
如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 个 | B. | 1个 | C. | 2 个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
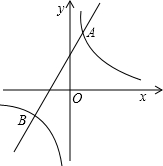 如图,直线y=x+m和双曲线y=$\frac{k}{x}$相交于点A(1,2)和点B(n,-1).
如图,直线y=x+m和双曲线y=$\frac{k}{x}$相交于点A(1,2)和点B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
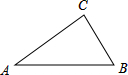 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com