
【题目】学习新知:如图 1、图 2,![]() 是矩形
是矩形![]() 所在平面内任意一点,则有以下重要结论:
所在平面内任意一点,则有以下重要结论: ![]() .该结论的证明不难,同学们通过勾股定理即可证明.
.该结论的证明不难,同学们通过勾股定理即可证明.
应用新知:如图 3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 内一点,且
内一点,且![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.

科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )

A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
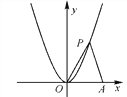
【题目】如图,点P是抛物线y=x2在第一象限内的一点,点A的坐标是(3,0).设点P的坐标为(x,y).
(1)求△OPA的面积S关于变量y的关系式;
(2)S是x的什么函数?
(3)当S=6时,求点P的坐标;
(4)在y=x2的图象上求一点P′,使△OP′A的两边OP′=P′A.
查看答案和解析>>
科目:初中数学 来源: 题型:
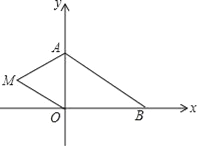
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.
(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣![]() 时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
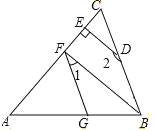
【题目】如图所示,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系?并说明理由;
(2)如果,DE⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,∠1+∠2=180°,∠A=∠C,试说明:AE∥BC.
解:因为∠1+∠2=180°,
所以AB∥ (同旁内角互补,两直线平行)
所以∠A=∠EDC( ),
又因为∠A=∠C(已知)
所以∠EDC=∠C(等量代换),
所以AE∥BC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校带领学生演出,参加演出的女生人数是男生人数的2倍少100人,学校需要采购一批演出服装.经了解:![]() 两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商:
两家制衣公司生产的这款演出服装的用料相同,单位也一样,男装都是120元一套,女装都是100元一食. 经洽谈协商:![]() 公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费;
公司给出的优惠条件是全部服装按单位打七折,但校方需承担2200元的运费;![]() 公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有
公司的优惠条件是男女装均按每套100元且打八折,公司承担运费.如果设参加演出的男生有![]() 人.
人.
(1)分别写出学校购买![]() 两公司服装所付的总费用
两公司服装所付的总费用![]() (元)和
(元)和![]() (元)与参演男生人数
(元)与参演男生人数![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)当参演男生人数是100人时,学校选用哪家制衣公司合算?当参演男生人数是300人时,学校选用哪家制衣公司合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com