练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在矩形ABCD中，AB=6，BC=11，若分别以点A、C为圆心的两圆相外切，点D在⊙C内，点B在⊙C外，则⊙A半径r的取值范围为
     
    ．
    考点：点与圆的位置关系
    专题：
    分析：首先根据点D在⊙C内，点B在⊙C外，求得⊙C的半径是大于6而小于11；再根据勾股定理求得AC的长，最后根据两圆的位置关系得到其数量关系．
    解答：解：∵在矩形ABCD中，AB=6，BC=11，
    ∴AC=
    		AB2+BC2
    =
    		157
    ，
    ∵点D在⊙C内，点B在⊙C外，
    ∴⊙C的半径R的取值范围为：6＜R＜11，
    ∵⊙A和⊙C外切，圆心距等于两圆半径之和是
    		157
    ，设⊙C的半径是Rc，即Rc+r=
    		157
    ，
    ∴半径r的取值范围是：
    		157
    -11＜r＜
    		157
    -6．
    故答案为：
    		157
    -11＜r＜
    		157
    -6．
    点评：此题考查了点与圆的位置关系以及勾股定理，利用两圆的位置关系与数量关系之间的等价关系是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知AD是△ABC的底边上高，若AB-BD=AC-CD，求证：△ABC为等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，等腰△ABC中，若AC=BC，且∠ADP=∠BPE，求证：△APD∽△BEP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知物体的三视图如图所示，描述物体的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，小岛P的周围20
    		2
    海里内有暗礁，某渔船沿北偏东61°的AM方向航行，在A处测得小岛P的方向为北偏东30°，且距A处40海里，该渔船若不改变航向，有无触礁的可能？若有可能触礁，则该渔船在A处应再向北偏东至少偏离多大角度才能脱险？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

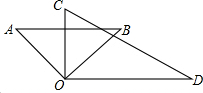    如图，将一副三角板的直角顶点重合，摆放在桌面上．
    （1）若∠AOD=140°，则∠BOC=
     

    （2）若∠BOC=30°，则∠AOD=
     

    （3）通过（1）（2）两题的计算，你发现∠AOD与∠BOC有什么数量关系？并说明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知方程组
    mx-3y=-3
    5x-ny=-35
    ，由于甲看错了方程组中的n，解得
    x=1
    y=3
    ，乙看错了方成组中的m．得到
    x=11
    y=2
    ，请你帮助他们按正确的m、n解原方程组．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个几何体的三视图如图所示，则这个几何体的表面积是
     
    cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

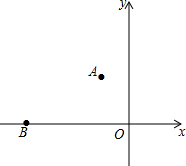    如图所示，某警察在点A（-2，4）接到任务，前去阻截在点B（-10，0）的劫包摩托车，劫包摩托车从点B沿x轴向原点方向匀速行驶，警察立即拦下一辆摩托车前去阻截，若两辆摩托车行驶速度相等，则相遇时警察的坐标为
     
    ．

    查看答案和解析>>

    同步练习册答案