
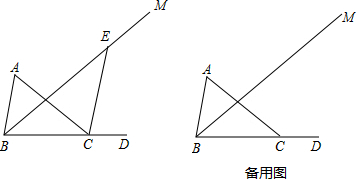
分析 (1)①根据三角形的内角和得到∠ABC=80°,由角平分线的定义得到∠ABE=$\frac{1}{2}∠$ABC=40°,根据平行线的性质即可得到结论;
②根据邻补角的定义得到∠ACD=180°-∠ACB=140°,根据角平分线的定义得到∠CBE=$\frac{1}{2}∠$ABC=40°,∠ECD=$\frac{1}{2}$ACD=70°,根据三角形的外角的性质即可得到结论;
(2)①当CE⊥BC时,②如图2,当CE⊥AB于F时,③如图3,当CE⊥AC时,根据垂直的定义和三角形的内角和即可得到结论.
解答 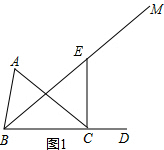 解:(1)①∵∠A=60°,∠ACB=40°,
解:(1)①∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,
∵BM平分∠ABC,
∴∠ABE=$\frac{1}{2}∠$ABC=40°,
∵CE∥AB,
∴∠BEC=∠ABE=40°;
②∵∠A=60°,∠ACB=40°,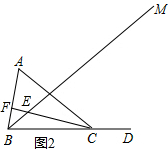
∴∠ABC=80°,∠ACD=180°-∠ACB=140°,
∵BM平分∠ABC,CE平分∠ACD,
∴∠CBE=$\frac{1}{2}∠$ABC=40°,∠ECD=$\frac{1}{2}$ACD=70°,
∴∠BEC=∠ECD-∠CBE=30°;
(2)①如图1,当CE⊥BC时,
∵∠CBE=40°,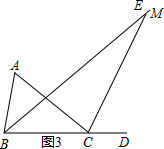
∴∠BEC=50°;
②如图2,当CE⊥AB于F时,
∵∠ABE=40°,
∴∠BEC=90°+40°=130°,
③如图3,当CE⊥AC时,
∵∠CBE=40°,∠ACB=40°,
∴∠BEC=180°-40°-40°-90°=10°.
点评 本题考查了平行线的性质,角平分线的定义,垂直的定义,三角形的内角和,三角形的外角的性质,正确的画出图形是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
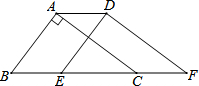 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
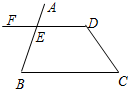 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 已知①②则③ | B. | 已知②⑤则④ | C. | 已知②④则③ | D. | 已知④⑤则② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com