
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
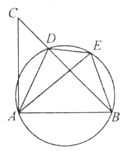
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
【答案】(1)证明见解析;(2)BC=![]()
【解析】分析: (1)由翻折的性质得出△ADE≌△ADC,根据全等三角形对应角相等,对应边相等得出∠AED=∠ACD,AE=AC,根据同弧所对的圆周角相等得出∠ABD=∠AED,根据等量代换得出∠ABD=∠ACD,根据等角对等边得出AB=AC,从而得出结论;
(2)如图,过点A作AH⊥BE于点H,根据等腰三角形的三线合一得出BH=EH=1,根据等腰三角形的性质及圆周角定理得出∠ABE=∠AEB=ADB,根据等角的同名三角函数值相等及余弦函数的定义得出BH∶AB = 1∶3,从而得出AC=AB=3,在Rt三角形ABC中,利用勾股定理得出BC的长.
详解:
(1)解 :由题意得△ADE≌△ADC,
∴∠AED=∠ACD,AE=AC
∵∠ABD=∠AED,
∴∠ABD=∠ACD
∴AB=AC
∴AE=AB
(2)解 :如图,过点A作AH⊥BE于点H
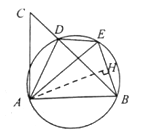
∵AB=AE,BE=2
∴BH=EH=1
∵∠ABE=∠AEB=ADB,cos∠ADB=![]()
∴cos∠ABE=cos∠ADB=![]()
∴ ![]() =
=![]()
∴AC=AB=3
∵∠BAC=90°,AC=AB
∴BC= ![]()


科目:初中数学 来源: 题型:
【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
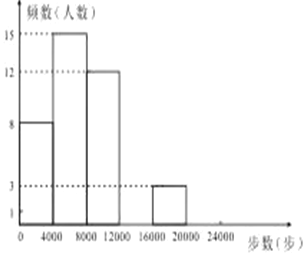
请根据以上信息,解答下列问题:
(1)写出![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)本市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步的两名教师与大家分享心得,求被选取的两名教师恰好都在
步的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
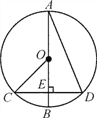
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知三角形纸片![]() ,将纸片折叠,使点
,将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() 交于点
交于点![]() .
.
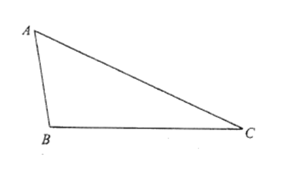
(1)画出直线![]() ;
;
(2)若点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,请画出点
,请画出点![]() ;
;
(3)在(2)的条件下,联结![]() ,如果
,如果![]() 的面积为2,
的面积为2,![]() 的面积为
的面积为![]() ,那么
,那么![]() 的面积等于 .
的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com